27. I concetti fondamentali che abbiamo introdotto fino a questo punto sono quello che serve per discutere le applicazioni analitiche della potenziometria. Come abbiamo gia' accennato (punto 11) la chiave di volta e' l'equazione di Nernst, che fornisce il legame fra il potenziale elettrodico e la concentrazione in soluzione di un dato analita.
Abbiamo pero' imparato che cio' che si puo' misurare e' in realta' solo una differenza fra potenziali elettrodici e quindi una determinazione analitica per via potenziometrica richiede invariabilmente l'allestimento di una cella elettrochimica completa: uno dei due elettrodi sara' un elettrodo di riferimento, mentre l'altro, il cui potenziale e' utilizzato ai fini analitici, viene detto elettrodo indicatore.
28. La potenziometria diretta consiste nella determinazione della concentrazione di un analita da una singola misura di differenza di potenziale in una cella.
29.
Un esempio di questo tipo di applicazione e' la
determinazione dello ione ![]() . Abbiamo una soluzione test che
contiene una concentrazione incognita di ioni
. Abbiamo una soluzione test che
contiene una concentrazione incognita di ioni ![]() ; se immergiamo
un filo di argento in questa soluzione otteniamo un elettrodo ad
; se immergiamo
un filo di argento in questa soluzione otteniamo un elettrodo ad
![]() , il cui potenziale e' legato proprio alla concentrazione
che dobbiamo determinare dalla relazione
(punto 13):
, il cui potenziale e' legato proprio alla concentrazione
che dobbiamo determinare dalla relazione
(punto 13):
![\begin{eqnarray*}
E_{Ag^+/Ag}&=&E^{\circ}_{Ag^+/Ag}+\frac{RT}{F}\ln\left[Ag^+\right]\\
\end{eqnarray*}](img153.gif)
Il potenziale di questo elettrodo, che rappresenta quindi il nostro elettrodo indicatore, puo' essere misurato solo relativamente ad un elettrodo di riferimento e quindi dovremo allestire una cella come quella mostrata nella figura 1.10.
La differenza di potenziale che si puo' misurare con il voltmetro e' data da:
dove ![]() e' il potenziale elettrodico dell'elettrodo
indicatore,
e' il potenziale elettrodico dell'elettrodo
indicatore, ![]() quello dell'elettrodo di riferimento (non ha
importanza specificare di che tipo; potrebbe essere un calomelano o un
quello dell'elettrodo di riferimento (non ha
importanza specificare di che tipo; potrebbe essere un calomelano o un
![]() ) e
) e ![]() e' la somma di tutti i contributi dovuti
ai potenziali di giunto (dalla figura si vede che ci sono due
potenziali di giunto in corrispondenza al contatto delle due
estremita' del ponte salino con le due soluzioni elettrodiche). Se
scriviamo la forma esplicita di
e' la somma di tutti i contributi dovuti
ai potenziali di giunto (dalla figura si vede che ci sono due
potenziali di giunto in corrispondenza al contatto delle due
estremita' del ponte salino con le due soluzioni elettrodiche). Se
scriviamo la forma esplicita di ![]() con la legge di Nernst
ed isoliamo la concentrazione di ioni argento otteniamo:
con la legge di Nernst
ed isoliamo la concentrazione di ioni argento otteniamo:
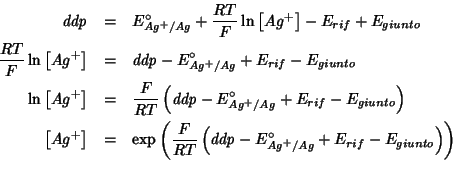
da cui si vede che, misurando ![]() con il voltmetro e
con il voltmetro e
![]() con un termometro e conoscendo il resto, possiamo ottenere la
concentrazione cercata. Va notato che, mentre i potenziali standard
e i potenziali elettrodici degli elettrodi di riferimento piu' comuni
sono tabulati con buona precisione, la misura o il calcolo dei
potenziali di giunto presentano notevoli difficolta'. Quindi, in
questo caso, il termine
con un termometro e conoscendo il resto, possiamo ottenere la
concentrazione cercata. Va notato che, mentre i potenziali standard
e i potenziali elettrodici degli elettrodi di riferimento piu' comuni
sono tabulati con buona precisione, la misura o il calcolo dei
potenziali di giunto presentano notevoli difficolta'. Quindi, in
questo caso, il termine
![]() rappresenta
sicuramente una possibile fonte di errore, tanto piu' in quanto
compare in un termine esponenziale. D'altro canto, per la cella
mostrata, c'e' da aspettarsi che i potenziali di giunto che si originano
alle due estremita' del ponte salino siano di segno contrario e
tendano quindi a cancellarsi.
rappresenta
sicuramente una possibile fonte di errore, tanto piu' in quanto
compare in un termine esponenziale. D'altro canto, per la cella
mostrata, c'e' da aspettarsi che i potenziali di giunto che si originano
alle due estremita' del ponte salino siano di segno contrario e
tendano quindi a cancellarsi.
30.
La cella di figura 1.10 puo' essere adoperata
per la determinazione analitica di moltissimi ioni metallici: basta
semplicemente cambiare il metallo dell'elettrodo indicatore. Ad
esempio, se invece di un filo di argento utilizziamo un filo di rame,
possiamo dosare gli ioni ![]() . In questo caso il potenziale
elettrodico dell'elettrodo indicatore e' dato da:
. In questo caso il potenziale
elettrodico dell'elettrodo indicatore e' dato da:
![\begin{eqnarray*}
E_{Cu^{2+}/Cu}&=&E^{\circ}_{Cu^{2+}/Cu}+\frac{RT}{2F}\ln\left[Cu^{2+}\right]\\
\end{eqnarray*}](img160.gif)
e la differenza di potenziale che si puo' misurare con il voltmetro e' data da:
da cui, identicamente a quanto visto prima, si puo' ricavare la
concentrazione incognita di ioni ![]() .
.
31.
Le possibilita' dei metodi potenziometrici non sono certo
limitate ai cationi metallici: esistono elettrodi indicatori per la
determinazione di moltissime specie. Un esempio di elettrodo
indicatore utilizzabile per gli ioni ![]() e' l'elettrodo ad
e' l'elettrodo ad
![]() . Ne abbiamo parlato a piu' riprese
(punto 3, pagina
. Ne abbiamo parlato a piu' riprese
(punto 3, pagina ![]() ,
punto 20) e lo abbiamo citato come esempio di
elettrodo di riferimento molto usato.
,
punto 20) e lo abbiamo citato come esempio di
elettrodo di riferimento molto usato.
Riscriviamo la legge di Nernst per questo elettrodo:
Questa relazione dice che, se la concentrazione di ioni ![]() e'
mantenuta costante, allora il potenziale elettrodico rimarra' costante
e su questo si basa l'impiego dell'elettrodo ad
e'
mantenuta costante, allora il potenziale elettrodico rimarra' costante
e su questo si basa l'impiego dell'elettrodo ad ![]() come
riferimento. Tuttavia, la relazione su scritta puo' essere intesa
anche in senso ``analitico'' considerando la concentrazione di ioni
come
riferimento. Tuttavia, la relazione su scritta puo' essere intesa
anche in senso ``analitico'' considerando la concentrazione di ioni
![]() come un'incognita da trovare misurando il potenziale
elettrodico.
come un'incognita da trovare misurando il potenziale
elettrodico.
Al solito, si dovra' allestire una cella come quella mostrata in
figura 1.11 e misurare la differenza di potenzaile fra
l'elettrodo indicatore e quello di riferimento (che potrebbe essere
anch'esso un elettrodo ad ![]() !):
!):
Da questa relazione si ricava, analogamente a quanto abbiamo gia'
visto, la concentrazione incognita di ioni ![]() .
.
32. L'allestimento di una cella elettrochimica completa per effettuare una misura potenziometrica puo' essere di gran lunga semplificato utilizzando un cosiddetto elettrodo combinato. Si tratta di un sistema compatto che contiene l'elettrodo indicatore insieme all'elettrodo di riferimento in un unico assemblaggio: immergendo l'elettrodo combinato nella soluzione test si realizza una cella elettrochimica completa. E' importante rendersi conto che un elettrodo combinato immerso nella soluzione test e' perfettamente equivalente ad una cella elettrochimica ``convenzionale'', cioe' del tipo che abbiamo illustrato finora. La figura 1.12 mostra la ``metamorfosi'' che porta da una cella usuale ad un elettrodo combinato.
Nello stadio 1 si vede la cella elettrochimica ``convenzionale'':
``I'' sta ad indicare la semicella dell'elettrodo indicatore (ad
esempio il solito filo di ![]() ) contenente la soluzione test; ``R''
indica la semicella dell'elettrodo di riferimento (ad esempio
un elettrodo ad
) contenente la soluzione test; ``R''
indica la semicella dell'elettrodo di riferimento (ad esempio
un elettrodo ad ![]() con una soluzione satura di
con una soluzione satura di ![]() ). Le
due semicelle sono separate da un setto poroso indicato dalla linea
tratteggiata. Infine, e' mostrato un voltmetro che misura la
differenza di potenziale della cella.
). Le
due semicelle sono separate da un setto poroso indicato dalla linea
tratteggiata. Infine, e' mostrato un voltmetro che misura la
differenza di potenziale della cella.
Il primo passo per arrivare all'assemblaggio combinato consiste nel prendere (idealmente) la semicella di riferimento e immergerla nella semicella dell'elettrodo indicatore: si arriva cosi' allo stadio 2. Naturalmente, per mantenere il contatto elettrico fra le due semicelle, nella semicella di riferimento e' presente una ``finestra'' costituita dal setto poroso (indicata con la linea tratteggiata nella figura). Notate che, nella sostanza, non e' cambiato nulla; solo la forma della cella e' cambiata.
Nello stadio successivo, il numero 3, abbiamo preso il metallo
dell'elettrodo indicatore e lo abbiamo messo in contatto con la
soluzione test, ma facendolo passare attraverso la semicella di
riferimento. Ovviamente, siccome il metallo dell'elettrodo indicatore
deve stare in contatto solo con la soluzione test (e non con la
soluzione dell'elettrodo di riferimento) la parte di metallo che passa
attraverso la soluzione dell'elettrodo di riferimento e' stata
opportunamente isolata inserendola all'interno di uno stretto tubo in
vetro (indicato in grigio nella figura). Un altro cambiamento che si
e' verificato nel passaggio da 2 a 3 riguarda il setto poroso, che si
ridotto ad una finestrella avente le dimensioni di ![]() . Di
nuovo: solo la forma sta cambiando, ma le varie parti e la loro
connessione rimangono inalterate.
. Di
nuovo: solo la forma sta cambiando, ma le varie parti e la loro
connessione rimangono inalterate.
Nello stadio 4 la metamorfosi si e' conclusa: l'elettrodo combinato e' completato da un coperchio superiore da cui escono i cavi collegati al riferimento e all'elettrodo indicatore. Inoltre, e' stato aggiunto un piccolo raccordo in vetro con tappo che serve per aggiungere soluzione (all'occorrenza) nella semicella di riferimento.
A questo punto, dovrebbe esservi chiaro che l'elettrodo combinato immerso nella soluzione test dello stadio numero 4 e' perfettamente equivalente alla cella ``convenzionale'' dello stadio numero 1 da cui siamo partiti.
33.
Immaginiamo di compiere una titolazione di ioni ![]() con
una soluzione standard di
con
una soluzione standard di ![]() . Nel corso della titolazione la
concentrazione di ioni
. Nel corso della titolazione la
concentrazione di ioni ![]() in soluzione varia: prima del punto di
equivalenza essa sara' molto piccola poiche' gli ioni
in soluzione varia: prima del punto di
equivalenza essa sara' molto piccola poiche' gli ioni ![]() sono in
eccesso; al punto di equivalenza la concentrazione degli ioni
sono in
eccesso; al punto di equivalenza la concentrazione degli ioni ![]() subisce un brusco incremento poiche' gli ioni
subisce un brusco incremento poiche' gli ioni ![]() ``finiscono'';
dopo il punto di equivalenza, la concentrazione di ioni
``finiscono'';
dopo il punto di equivalenza, la concentrazione di ioni ![]() aumenta all'aumentare del volume di soluzione titolante aggiunto.
aumenta all'aumentare del volume di soluzione titolante aggiunto.
Sulla base di quello che abbiamo appreso finora, possiamo comprendere
facilmente che, se immergiamo un filo di argento nel beaker in cui
stiamo conducendo la titolazione, realizziamo un elettrodo ad
![]() il cui potenziale seguira' le variazioni di
concentrazione degli ioni argento nel corso della titolazione.
il cui potenziale seguira' le variazioni di
concentrazione degli ioni argento nel corso della titolazione.
Una titolazione potenziometrica, dunque, consiste in una titolazione ordinaria in cui la misura potenziometrica viene utilizzata per monitorare il corso della titolazione.
Se vogliamo seguire la titolazione di ![]() con
con ![]() per via
potenziometrica non e' sufficiente immergere un filo d'argento nel
beaker contenente la soluzione da titolare: sappiamo che oltre
all'elettrodo indicatore abbiamo bisogno di un elettrodo di
riferimento rispetto al quale misurare il potenziale del
primo. Dovremo percio' allestire una cella
(figura 1.13) o, piu' comodamente, usare un
elettrodo combinato (figura 1.14).
per via
potenziometrica non e' sufficiente immergere un filo d'argento nel
beaker contenente la soluzione da titolare: sappiamo che oltre
all'elettrodo indicatore abbiamo bisogno di un elettrodo di
riferimento rispetto al quale misurare il potenziale del
primo. Dovremo percio' allestire una cella
(figura 1.13) o, piu' comodamente, usare un
elettrodo combinato (figura 1.14).
Come abbiamo gia' visto piu' volte, la differenza di potenziale misurata dal voltmetro e' data da:
![\begin{eqnarray*}
\mathit{ddp}&=&E_{Ag^+/Ag}-E_{rif}+E_{giunto}\\
&=&E^\circ_{Ag^+/Ag}+\frac{RT}{F}\ln\left[Ag^+\right]-E_{rif}+E_{giunto}\\
\end{eqnarray*}](img168.gif)
Come abbiamo detto prima, la concentrazione di ioni ![]() cambia in
funzione del volume di soluzione titolante aggiunto: la relazione su
scritta mostra che la differenza di potenziale della cella riflettera'
questo cambiamento. Possiamo allora costruire una tabella in cui, per
ogni valore del volume di titolante aggiunto, riportiamo il
corrispondente valore di differenza di potenziale letto dal
voltmetro. Diagrammando i dati cosi' raccolti otterremo una tipica
curva di titolazione di forma sigmoide: il flesso di
tale curva, facilmente determinabile, come vedremo, individua cio' che
rappresenta lo scopo della titolazione, e cioe' il volume di
equivalenza (figura 1.15).
cambia in
funzione del volume di soluzione titolante aggiunto: la relazione su
scritta mostra che la differenza di potenziale della cella riflettera'
questo cambiamento. Possiamo allora costruire una tabella in cui, per
ogni valore del volume di titolante aggiunto, riportiamo il
corrispondente valore di differenza di potenziale letto dal
voltmetro. Diagrammando i dati cosi' raccolti otterremo una tipica
curva di titolazione di forma sigmoide: il flesso di
tale curva, facilmente determinabile, come vedremo, individua cio' che
rappresenta lo scopo della titolazione, e cioe' il volume di
equivalenza (figura 1.15).
34.
Le titolazioni potenziometriche presentano dei vantaggi
rispetto alle misure potenziometriche dirette. Siccome il punto finale
viene determinato dal flesso della curva di titolazione, non
e' necessario conoscere con esattezza il potenziale dell'elettrodo di
riferimento (diversamente da quanto avviene invece in una misura
potenziometrica diretta). Infatti, dall'espressione della differenza
di potenziale prima scritta, si vede che il termine ![]() interviene come un semplice addendo: cio' vuol dire che il suo effetto
e' semplicemente quello di traslare verticalmente la curva di
titolazione. Ma questo non ha alcuna influenza sulla posizione del
flesso lungo l'asse delle ascisse. Un altro vantaggio delle
titolazioni potenziometriche rispetto alle misure dirette riguarda il
potenziale di giunto (
interviene come un semplice addendo: cio' vuol dire che il suo effetto
e' semplicemente quello di traslare verticalmente la curva di
titolazione. Ma questo non ha alcuna influenza sulla posizione del
flesso lungo l'asse delle ascisse. Un altro vantaggio delle
titolazioni potenziometriche rispetto alle misure dirette riguarda il
potenziale di giunto (
![]() nell'espressione piu'
sopra). Questo, come sappiamo, e' difficile da misurare o calcolare e
quindi rappresenta una fonte di errore ineliminabile. Tuttavia, la
variazione del potenziale di giunto durante una titolazione e'
sicuramente molto piccola: in altre parole, i valori di differenza di
potenziale che leggiamo nel corso di una titolazione sono affetti da
un errore uguale per tutti. Come per il termine
nell'espressione piu'
sopra). Questo, come sappiamo, e' difficile da misurare o calcolare e
quindi rappresenta una fonte di errore ineliminabile. Tuttavia, la
variazione del potenziale di giunto durante una titolazione e'
sicuramente molto piccola: in altre parole, i valori di differenza di
potenziale che leggiamo nel corso di una titolazione sono affetti da
un errore uguale per tutti. Come per il termine ![]() ,
cio' determina solo una traslazione verticale della curva di
titolazione, senza alcuna conseguenza nella determinazione del punto
finale.
,
cio' determina solo una traslazione verticale della curva di
titolazione, senza alcuna conseguenza nella determinazione del punto
finale.
35. Qualsiasi titolazione puo' essere seguita per via potenziometrica: e' sufficiente disporre di un elettrodo indicatore il cui potenziale dipenda dalla concentrazione di una delle specie chimiche che partecipano alla reazione su cui la titolazione e' basata. Citiamo qualche ulteriore esempio.
Nel corso della titolazione il rapporto fra la concentrazione dello
ione ![]() e quella dello ione
e quella dello ione ![]() passa da un valore
iniziale molto piccolo ad un valore molto grande dopo il punto di
equivalenza (quando praticamente tutti gli ioni
passa da un valore
iniziale molto piccolo ad un valore molto grande dopo il punto di
equivalenza (quando praticamente tutti gli ioni ![]() sono stati
ossidati). Se immergiamo un filo di platino nella soluzione, otteniamo
un sistema elettrodico il cui potenziale dipende proprio dal rapporto
delle concentrazioni dei due ioni ferro
(pagina
sono stati
ossidati). Se immergiamo un filo di platino nella soluzione, otteniamo
un sistema elettrodico il cui potenziale dipende proprio dal rapporto
delle concentrazioni dei due ioni ferro
(pagina ![]() ) e che quindi puo' essere sfruttato per
seguire la titolazione:
) e che quindi puo' essere sfruttato per
seguire la titolazione:
36. Come abbiamo detto, al termine di una titolazione potenziometrica ci ritroviamo con una tabella in cui, per ogni valore del volume di soluzione titolante, abbiamo riportato la corrispondente differenza di potenziale letta sul voltmetro. La prima cosa da fare e' costruire un grafico in cui si riporta la differenza di potenziale in funzione del volume di titolante.
Una volta costruita la curva di titolazione, si pone il problema della determinazione del punto finale, corrispondente al flesso della curva.
La cosa piu' semplice e' quella di stimare ad occhio la posizione del flesso. Quando il salto della curva in corrispondenza al punto finale e' sufficientemente netto, la precisione del risultato ottenibile con questo sistema e' sicuramente comparabile con quella fornita da metodi piu' sofisticati.
Fra i tanti metodi grafici sviluppati a questo scopo, citiamo i seguenti due.
![\begin{psfrags}
\psfrag{dummy}{}
\psfrag{volume}[c][c]{volume di titolante}
\psf...
...{2}{2}
\psfrag{3}{3}
\psfrag{4}{4}
\includegraphics {endPoint1.eps}\end{psfrags}](img173.gif)
|
![\begin{psfrags}
\psfrag{dummy}{}
\psfrag{volume}[c][c]{volume di titolante}
\psf...
...{6}{6}
\psfrag{7}{7}
\psfrag{8}{8}
\includegraphics {endPoint2.eps}\end{psfrags}](img174.gif)
|
37.
Allo scopo di aumentare la precisione (ad esempio quando il
salto in corrispondenza del punto finale non e' molto netto) si
possono elaborare numericamente i dati ottenuti ricavando la derivata
prima e seconda della curva di titolazione. Al termine dell'esperienza
si e' in possesso di una sequenza di ![]() coppie di valori
coppie di valori
![]() . Allora e' possibile costruire una sequenza di
. Allora e' possibile costruire una sequenza di ![]() coppie di valori
coppie di valori
![]() , con:
, con:
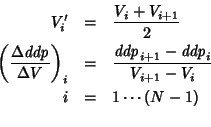
Notate che
![]() e' la pendenza della
retta che passa per i punti di coordinate
e' la pendenza della
retta che passa per i punti di coordinate
![]() e
e
![]() , e quindi rappresenta
un'approssimazione alla derivata prima della curva di titolazione nel
punto medio fra
, e quindi rappresenta
un'approssimazione alla derivata prima della curva di titolazione nel
punto medio fra ![]() e
e ![]() , cioe'
, cioe'
![]() . La
cosa e' illustrata nella figura 1.18.
. La
cosa e' illustrata nella figura 1.18.
Siccome la curva di titolazione ha un andamento sigmoide, la sua
derivata prima mostrera' un picco pronunciato in corrispondenza al
punto finale, che ne consente una piu' facile
determinazione. (Per rendervi conto di come la derivata prima di una
sigmoide sia una funzione a picco, considerate come varia la pendenza
di una retta tangente alla curva ![]() in figura 1.19 al
variare di
in figura 1.19 al
variare di ![]() )
)
Il procedimento puo' essere ripetuto per ottenere la derivata
seconda. A partire dalle ![]() coppie di valori
coppie di valori
![]() e' possibile ricavare
e' possibile ricavare ![]() coppie di
dati
coppie di
dati
![]() , con:
, con:
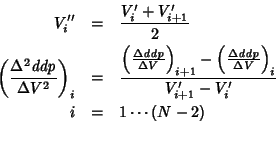
Siccome la derivata prima della curva di titolazione e' una funzione a picco, la sua derivata (cioe' la derivata seconda della curva di titolazione) sara' una funzione che presenta una brusca oscillazione che taglia l'asse delle ascisse in corrispondenza al punto finale (figura 1.19).
Nonostante questi metodi possano risultare accattivanti, va comunque tenuto presente che essi sono limitati dal livello di ``rumore'' associato ai dati sperimentali raccolti: l'operazione di derivazione comporta infatti un'inevitabile amplificazione degli errori sempre presenti nelle misure sperimentali, portandoli in molti casi a livelli inaccettabili.
Un esempio di applicazione di questo metodo a un caso reale e' mostrato nella figura 1.20.
38. Un approccio numerico completamente diverso all'analisi della curva di titolazione consiste nell'approssimazione della curva stessa con una opportuna funzione analitica.
L'idea si basa sulla seguente considerazione: siccome il nostro interesse e' quello di trovare il flesso della curva di titolazione, e' sufficiente scovare una funzione qualsiasi che segua bene l'andamento dei punti sperimentali in un intervallo non molto ampio e centrato intorno al punto di flesso. Una volta trovata una funzione simile, e' sufficiente farne la derivata seconda e porla uguale a zero: e' questa la ben nota (mi auguro!) condizione per un punto di flesso.
Uno fra i possibili modelli analitici in grado di riprodurre il tipico andamento di una curva di titolazione e' quello che segue:
Questa relazione esprime la differenza di potenziale misurata
![]() come funzione del volume di titolante
come funzione del volume di titolante ![]() . I
termini
. I
termini ![]() sono dei parametri: mentre le
caratteristiche generali della funzione sono determinate dalla sua
forma analitica, il suo aspetto particolare e' determinato dal
valore numerico dei parametri. Per comprendere cosa significhi cio',
facciamo un semplicissimo parallelo. Sappiamo tutti che la funzione:
sono dei parametri: mentre le
caratteristiche generali della funzione sono determinate dalla sua
forma analitica, il suo aspetto particolare e' determinato dal
valore numerico dei parametri. Per comprendere cosa significhi cio',
facciamo un semplicissimo parallelo. Sappiamo tutti che la funzione:
rappresenta una retta nel piano cartesiano. Questa (cioe' quella di
essere una retta) e' una caratteristica insita nel modello analitico,
indipendente dal particolare valore dei parametri, che in
questo caso sono ![]() , la pendenza, e
, la pendenza, e ![]() , l'intercetta. La forma
che abbiamo scritto sopra rappresenta una (doppia) infinita' di rette:
possiamo individuare una particolare retta di questo insieme
assegnando due particolari valori a
, l'intercetta. La forma
che abbiamo scritto sopra rappresenta una (doppia) infinita' di rette:
possiamo individuare una particolare retta di questo insieme
assegnando due particolari valori a ![]() e
e ![]() .
.
Cerchiamo di comprendere in modo qualitativo come e' fatto il modello proposto per approssimare le curve di titolazione. A questo scopo, e' utile riscriverlo come somma di due parti:
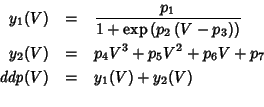
Il termine ![]() e' la parte piu' significativa del modello: esso
rappresenta una funzione sigmoide le cui caratteristiche dipendono dai
tre parametri
e' la parte piu' significativa del modello: esso
rappresenta una funzione sigmoide le cui caratteristiche dipendono dai
tre parametri ![]() . L'andamento di
. L'andamento di ![]() e' mostrato
nella figura 1.21: in pratica la funzione e' contenuta in una
``striscia'' delimitata dall'asse
e' mostrato
nella figura 1.21: in pratica la funzione e' contenuta in una
``striscia'' delimitata dall'asse ![]() e dalla retta orizzontale
e dalla retta orizzontale
![]() ; presenta un punto di flesso la cui posizione lungo l'asse
; presenta un punto di flesso la cui posizione lungo l'asse
![]() coincide con il parametro
coincide con il parametro ![]() ; restringendoci ai soli valori
positivi del parametro
; restringendoci ai soli valori
positivi del parametro ![]() , la funzione e' crescente se
, la funzione e' crescente se ![]() e decrescente se
e decrescente se ![]() ; infine, la ``ripidezza'' del salto
compiuto dalla funzione in corrispondenza al punto di flesso e'
proporzionale al valore assoluto di
; infine, la ``ripidezza'' del salto
compiuto dalla funzione in corrispondenza al punto di flesso e'
proporzionale al valore assoluto di ![]() (dovreste essere in grado
di verificare tutto cio' con le tecniche di analisi che avete appreso
alla scuola media superiore).
(dovreste essere in grado
di verificare tutto cio' con le tecniche di analisi che avete appreso
alla scuola media superiore).
 |
Il termine ![]() , che non e' altro che un polinomio di terzo
grado, e' stato introdotto per due motivi. Il primo e' che le curve di
titolazione sperimentali possono essere traslate arbitrariamente lungo
l'asse verticale mentre la funzione
, che non e' altro che un polinomio di terzo
grado, e' stato introdotto per due motivi. Il primo e' che le curve di
titolazione sperimentali possono essere traslate arbitrariamente lungo
l'asse verticale mentre la funzione ![]() tende inevitabilmente a
tende inevitabilmente a
![]() , per
, per
![]() o
o
![]() (a
seconda del segno di
(a
seconda del segno di ![]() e
e ![]() ):
): ![]() ha quindi il
compito di traslare opportunamente la sigmoide affinche' possa seguire
la curva sperimentale. Il secondo scopo del termine polinomiale e'
quello di aumentare le ``possibilita' di adattamento'' della sigmoide
all'andamento dei punti sperimentali.
ha quindi il
compito di traslare opportunamente la sigmoide affinche' possa seguire
la curva sperimentale. Il secondo scopo del termine polinomiale e'
quello di aumentare le ``possibilita' di adattamento'' della sigmoide
all'andamento dei punti sperimentali.
Come si procede in pratica? Alla fine dell'esperimento di titolazione
potenziometrica abbiamo un grafico della differenza di potenziale
misurata in funzione del volume di titolante aggiunto. A questo punto
il problema e' quello di determinare i valori dei parametri
![]() per i quali il modello analitico segue l'andamento
dei dati sperimentali nel modo migliore possibile. Problemi di
questo tipo sono detti di ``modellizzazione'' o ``best fit'' ed
esistono numerosissimi metodi per la loro soluzione (saro' lieto di
dare maggiori dettagli a chi sia interessato). In definitiva, i dati
sperimentali vengono immessi in un programma che realizza un
algoritmo tramite il quale i valori dei parametri vengono
iterativamente affinati finche' l'accordo fra modello e dati
sperimentali risulta il migliore possibile; a questo punto, il
programma risolve l'equazione:
per i quali il modello analitico segue l'andamento
dei dati sperimentali nel modo migliore possibile. Problemi di
questo tipo sono detti di ``modellizzazione'' o ``best fit'' ed
esistono numerosissimi metodi per la loro soluzione (saro' lieto di
dare maggiori dettagli a chi sia interessato). In definitiva, i dati
sperimentali vengono immessi in un programma che realizza un
algoritmo tramite il quale i valori dei parametri vengono
iterativamente affinati finche' l'accordo fra modello e dati
sperimentali risulta il migliore possibile; a questo punto, il
programma risolve l'equazione:
fornendo cosi' il valore del volume finale.
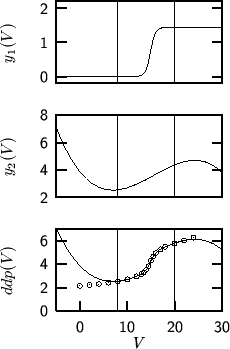
Nella figura 1.21 e' illustrato il procedimento di
ottimizzazione di cui stiamo parlando applicato ad un caso reale. Per
maggior chiarezza, i termini ottimizzati ![]() e
e ![]() sono
mostrati separatamente nei primi due grafici; nel terzo grafico i
circoletti sono i punti sperimentali mentre la linea continua e' il
grafico della funzione
sono
mostrati separatamente nei primi due grafici; nel terzo grafico i
circoletti sono i punti sperimentali mentre la linea continua e' il
grafico della funzione
![]() con i valori
ottimizzati dei parametri. Osservate come i dati sperimentali
descrivano una sigmoide compresa all'incirca fra
con i valori
ottimizzati dei parametri. Osservate come i dati sperimentali
descrivano una sigmoide compresa all'incirca fra ![]() e
e ![]() , mentre
la funzione
, mentre
la funzione ![]() , come detto prima, e' compresa fra
, come detto prima, e' compresa fra ![]() e
e
![]() : il termine
: il termine ![]() trasla la sigmoide portandola
sui punti sperimentali. Osservate ancora che l'accordo del modello con
i dati sperimentali e' piuttosto buono solo in un intervallo limitato
e centrato intorno al punto finale: al di fuori di questo intervallo
(si vede particolarmente bene per
trasla la sigmoide portandola
sui punti sperimentali. Osservate ancora che l'accordo del modello con
i dati sperimentali e' piuttosto buono solo in un intervallo limitato
e centrato intorno al punto finale: al di fuori di questo intervallo
(si vede particolarmente bene per ![]() ) la funzione
analitica non segue affatto i dati sperimentali. Questo non e' un
problema, visto che siamo interessati solo al punto di flesso della
curva di titolazione e quindi ci basta che la funzione coincida il
piu' possibile con la curva di titolazione solo in un intorno del
flesso.
) la funzione
analitica non segue affatto i dati sperimentali. Questo non e' un
problema, visto che siamo interessati solo al punto di flesso della
curva di titolazione e quindi ci basta che la funzione coincida il
piu' possibile con la curva di titolazione solo in un intorno del
flesso.