Relazione fra corrente e differenza di potenziale applicata

La corrente che circola nella cella durante l'elettrolisi e' funzione della differenza di potenziale applicata agli elettrodi e del tempo. In questa sezione ci occuperemo di indagare in maggiore dettaglio la dipendenza dalla differenza di potenziale, mentre lo studio di quella temporale viene per il momento rinviato. A tale scopo supporremo che il flusso di corrente che circola nella cella sia stazionario.

La variazione della corrente di elettrolisi col tempo e' dovuta essenzialmente alle variazioni di composizione causate dall'elettrolisi stessa e cioe' alla formazione o scomparsa di specie chimiche in seguito alle reazioni elettrodiche.^2.1 Nell'ipotesi di stazionarieta' possiamo immaginare che le specie prodotte per elettrolisi vengano continuamente rimosse dalla soluzione, mentre quelle consumate vengano continuamente rimpiazzate dall'esterno. In tali condizioni (realizzate ad esempio in una cella in flusso) la corrente dipende unicamente dalla differenza di potenziale applicata agli elettrodi ed e' appunto tale dipendenza che ci apprestiamo ora ad approfondire.

Si e' gia' visto che la differenza di potenziale da applicare deve essere almeno pari alla differenza fra i potenziali elettrodici di equilibrio: $E_{eq,A} - E_{eq,C}$. Tale limite e' imposto dalla termodinamica e rappresenta una differenza di potenziale appena sufficiente a controbilanciare la tendenza spontanea della reazione (2.5). Per poter osservare una corrente elettrica nel verso voluto, dovra' essere:

$$ddp> \left(E_{eq,A} - E_{eq,C}\right)$$

Il surplus di differenza di potenziale (rispetto al limite termodinamico su scritto) e' costituito da vari contributi che nel seguito cercheremo di evidenziare e spiegare.

Caduta ohmica

Cominciamo con l'osservare che la soluzione compresa fra i due elettrodi possiede una resistenza $R$ non trascurabile. Per forzare attraverso il circuito una corrente $i$ bisogna che la differenza di potenziale applicata contenga il termine necessario a vincere tale resistenza. Questo termine e' dato dalla legge di Ohm ed e' percio' detto caduta ohmica:

$$\mbox{%\input{ohm_drop.pstex_t}}$$

$$\Delta E_{ohm}=Ri$$ (2.8)

Va notato che la resistenza della soluzione e' funzione di diversi parametri, la composizione, la temperatura e la geometria della cella. Osserviamo ancora che il termine di caduta ohmica e' proporzionale alla corrente. Ad esempio, se durante l'elettrolisi si desidera sostenere una corrente di $50\;mA$ e la resistenza della soluzione (supposta costante) e' di $6\;\Omega$, la caduta ohmica risulta pari a $0.3\;V$.

Sulla base di quanto appena visto e di quanto detto nella sezione (2.1), possiamo scrivere la differenza di potenziale da applicare per ottenere il passaggio di una corrente $i$ nel modo seguente:

$$(ddp)_i=(E_A)_i-(E_C)_i+(\Delta E_{ohm})_i$$ (2.9)

L'indice ``i'' sta ad indicare che tutti i termini sono funzioni della corrente.

Il potenziale anodico e quello catodico possono essere espressi in termini dei rispettivi valori di equilibrio e dello spostamento $\eta$ da tali valori:

$$\eta_A = E_A-E_{eq,A}$$ (2.10)

$$\eta_C = E_C-E_{eq,C}$$ (2.11)

In tal modo:

$$(ddp)_i=\left(E_{eq,A}-E_{eq,C}\right)+\left((\eta_A)_i-(\eta_C)_i\right)+(\Delta E_{ohm})_i$$ (2.12)

La relazione (2.12) dice quale deve essere la differenza di potenziale da applicare per ottenere una corrente di elettrolisi $i$. Il termine $\left(E_{eq,A}-E_{eq,C}\right)$ non dipende da $i$ e rappresenta il valore che la differenza di potenziale deve avere per mantenere il sistema all'equilibrio ($i=0$). Vale tuttavia la pena di osservare che tale termine varia nel corso dell'elettrolisi a causa della variazione delle concentrazioni delle specie coinvolte nelle reazioni elettrodiche (si vedano le equazioni (2.3)-(2.4)).

I termini $\eta_A$ ed $\eta _C$ piu' sopra introdotti vengono detti rispettivamente sovratensione anodica e sovratensione catodica. Dalla combinazione delle equazioni (2.10)-(2.11) con le disuguaglianze (2.6)-(2.7) si deduce che quando il circuito della cella e' attraversato da una corrente $i$ si ha $\eta_A > 0$ ed $\eta_C<0$ . Il termine $\left((\eta_A)_i-(\eta_C)_i\right)$ e' dunque sempre positivo.

Nel seguito verra' approfondita la relazione fra corrente e sovratensione.

Cenni di cinetica elettrodica

In questa sezione ci occuperemo di indagare la dipendenza dalla corrente dei termini $\eta_A$ ed $\eta _C$ che compaiono nell'equazione (2.12).

Come si vedra', l'origine della sovratensione $\eta$ e' completamente indipendente dal fatto che un elettrodo funzioni da catodo o da anodo. Quindi, per affrontare la discussione in termini piu' generali possibile, concentriamo la nostra attenzione su una generica interfaccia elettrodica caratterizzata da un potenziale elettrodico $E$ e in presenza della coppia redox:

$$Ox+ne^-\rightleftharpoons Red$$

Se indichiamo con $C^*_{Ox}$ e $C^*_{Red}$ le concentrazioni massive^2.2 delle specie $Ox$ e $Red$, rispettivamente, allora sappiamo che il potenziale di equilibrio $E_{eq}$ dell'interfaccia e' dato dalla legge di Nernst:

$$E_{eq}=E^\circ_{Ox/Red}+\frac{RT}{nF}\ln\left(\frac{C^*_{Ox}}{C^*_{Red}}\right)$$ (2.13)

Quando $E=E_{eq}\;\;(\eta=0)$, la velocita' della reazione di riduzione:

$$Ox+ne^-\rightarrow Red$$

e' uguale a quella della reazione di ossidazione (sezione (1.1.3)):

$$Red\rightarrow Ox+ne^-$$

Il numero di elettroni (cariche) che attraversano l'interfaccia nell'unita' di tempo in un senso e in quello opposto e' lo stesso e la corrente netta risultante e' nulla.

Se $E\ne E_{eq}\;\;(\eta\ne0)$, una delle due reazioni procede piu' velocemente dell'altra e si ha una corrente netta risultante (catodica o di riduzione se $E<E_{eq}\;\;(\eta<0)$, anodica o di ossidazione se $E>E_{eq}\;\;(\eta>0)$)

La domanda a cui cercheremo di rispondere in questa sezione e' la seguente: se il potenziale elettrodico differisce di $\eta$ dal valore di equilibrio, quale sara' la corrispondente corrente netta $i$?

Cominciamo con l'osservare che la corrente netta $i$ misura in pratica la velocita' netta $v^\prime$ del processo elettrodico globale. Infatti, se indichiamo con $N$ le moli di $Ox$ ridotte (corrente netta catodica) o quelle di $Red$ ossidate (corrente netta anodica), allora (F e' la costante di Faraday):

$$i = \frac{dq}{dt}$$ (2.14)

$$= \frac{d(NnF)}{dt}$$

$$= nF\frac{dN}{dt}$$

$$= nFv^\prime$$ (2.15)

Siccome il processo elettrodico e' di tipo eterogeneo, cioe' e' spazialmente localizzato all'interfaccia elettrodo/soluzione, la sua velocita' globale e' direttamente proporzionale all'area $A$ di tale interfaccia. Si puo' pertanto definire una velocita' per unita' di area interfacciale (dimensioni $mol\; s^{-1}\; cm^{-2}$):

$$v=\frac{v^\prime}{A}$$

per cui:

$$i=nFAv \\$$ (2.16)

Il problema si sposta dunque alla determinazione della relazione fra $v$ ed $\eta$ .

In generale, un processo elettrodico e' costituito da diversi stadi. Nel caso piu' semplice tali stadi sono tre (figura 2.2):

Figura 2.2: Schematica rappresentazione del piu' semplice processo elettrodico (caso particolare di una riduzione n-elettronica): la specie $Ox$ raggiunge la superficie elettrodica, acquista $n$ elettroni e si trasforma in specie $Red$, che abbandona la superficie elettrodica ritornando nella massa della soluzione

1. il trasporto del reagente dalla massa della soluzione alla superficie elettrodica

2. il trasferimento elettronico eterogeneo fra la specie attiva presente sulla superficie elettrodica e l'elettrodo
3. il trasporto del prodotto dalla superficie elettrodica alla massa della soluzione

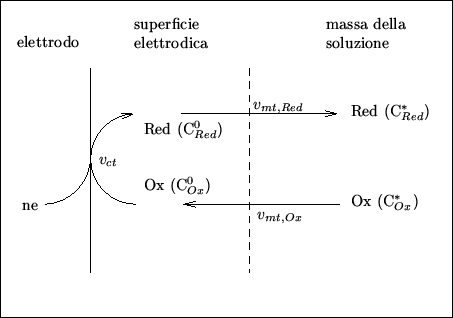In generale, la velocita' globale con cui avviene il processo elettrodico (cioe', per l'equazione (2.16), la corrente netta $i$) e' uguale alla piu' bassa delle velocita' individuali di questi tre stadi.

In particolare, e' importante realizzare che, in condizioni stazionarie, cioe' quelle che stiamo qui considerando, cfr. sezione (2.2), detta $v_{mt,Ox}$ la velocita' con cui si muovono le specie ossidate, $v_{mt,Red}$ quella con cui si muovono le specie ridotte e $v_{ct}$ la velocita' del trasferimento elettronico, deve valere:

$$\frac{i}{nFA}=v=v_{mt,Ox}=v_{mt,Red}=v_{ct}$$ (2.17)

Nel seguito ci occuperemo di mettere in relazione $v_{mt,Ox}$, $v_{mt,Red}$ e $v_{ct}$ (e quindi $i$) col potenziale elettrodico.

Il trasporto di massa in condizioni stazionarie

La reazione elettrodica altera la composizione della soluzione alla superficie dell'elettrodo. Cio' comporta l'instaurarsi di gradienti di concentrazione che determinano il movimento di specie chimiche dalla superficie elettrodica alla soluzione e viceversa (cio' e' una conseguenza della legge generale per cui se la concentrazione di una specie chimica in una soluzione non e' spazialmente omogenea, essa tendera' a spostarsi dalle regioni piu' concentrate a quelle meno concentrate).

Consideriamo la nostra interfaccia elettrodica mentre e' attraversata da una corrente stazionaria $i$. In tali condizioni le concentrazioni superficiali delle specie $Ox$ e $Red$ ($C^\circ_{Ox}$ e $C^\circ_{Red}$, rispettivamente) saranno diverse da quelle massive $C^*_{Ox}$ e $C^*_{Red}$, a causa della reazione elettrodica (se la corrente netta e' di tipo catodico si avra': $C^\circ_{Ox}<C^*_{Ox}$ e $C^\circ_{Red}>C^*_{Red}$; se invece la corrente netta e' di tipo anodico, si avra': $C^\circ_{Ox}>C^*_{Ox}$ e $C^\circ_{Red}<C^*_{Red}$). Come detto sopra, questa disomogeneita' spaziale di concentrazione provoca il movimento di molecole $Ox$ e $Red$ dalla superficie elettrodica alla soluzione e viceversa. La velocita' $v_{mt}$ di tale movimento e' approssimativamente proporzionale alla differenza fra la concentrazione massiva e quella superficiale:

$$v_{mt,Ox} = m_{Ox}\left(C^*_{Ox}-C^\circ_{Ox}\right)$$ (2.18)

$$v_{mt,Red} = m_{Red}\left(C^\circ_{Red}-C^*_{Red}\right)$$ (2.19)

$m_{Ox}$ ed $m_{Red}$ sono detti coefficienti di trasferimento di massa e danno una misura di quanto rapidamente si spostano le molecole di $Ox$ e $Red$, rispettivamente.

Tanto per fissare le idee consideriamo il caso di una corrente netta di riduzione (il caso opposto e' perfettamente analogo).

La situazione e' la seguente (figura 2.2):

1. molecole di $Ox$ si muovono, a velocita' $v_{mt,Ox}$, dalla soluzione verso l'elettrodo

2. alla superficie elettrodica acquistano $n$ elettroni e si trasformano in molecole $Red$ ad una velocita' $v_{ct}$

3. le molecole $Red$ si allontanano dalla superficie elettrodica verso la soluzione a velocita' $v_{mt,Red}$

In condizioni di stazionarieta', la velocita' di questi tre stadi deve essere la stessa. In particolare deve valere:

$$i=nFAv_{mt,Ox}=nFAv_{mt,Red}$$ (2.20)

Osserviamo a questo punto che la definizione di $v_{mt,Ox}$ e $v_{mt,Red}$ (equazioni (2.18) e (2.19)) implica la convenzione elettrochimica secondo cui una corrente netta di riduzione ( $C^\circ_{Ox}<C^*_{Ox}$ e $C^\circ_{Red}>C^*_{Red}$) e' positiva, mentre un corrente netta di ossidazione ( $C^\circ_{Ox}>C^*_{Ox}$ e $C^\circ_{Red}<C^*_{Red}$) e' negativa.

Osserviamo ancora che la velocita' con cui la specie $Ox$ puo' raggiungere l'elettrodo non e' illimitata: essa raggiunge un valore massimo quando $C^\circ_{Ox}\rightarrow 0$ (equazione (2.18)). La corrente di riduzione $i_{l,C}$ che si ha in tali condizioni e' detta corrente limite catodica ed e' data da:

$$i_{l,C}=nFAm_{Ox}C^*_{Ox}$$ (2.21)

Tale corrente rappresenta dunque la massima corrente catodica realizzabile nelle condizioni date.

In modo del tutto analogo si puo' vedere che, nel caso di una reazione netta di ossidazione, la massima corrente anodica raggiungibile e' data da:

$$i_{l,A}=-nFAm_{Red}C^*_{Red}$$ (2.22)

(si ricordi che, per convenzione, le correnti anodiche sono negative).

Combinando le equazioni (2.18)-(2.22) si ottiene:

$$\frac{C^\circ_{Ox}}{C^*_{Ox}} = 1-\frac{i}{i_{l,C}}$$ (2.23)

$$\frac{C^\circ_{Red}}{C^*_{Red}} = 1-\frac{i}{i_{l,A}}$$ (2.24)

Le due relazioni su scritte rappresentano il risultato finale di questa sezione: esse esprimono la dipendenza della corrente (stazionaria) dal trasporto di massa in soluzione.

Osserviamo che lo scopo finale di questa trattazione e' quello di ricavare una relazione fra $i$ ed $\eta$, mentre le equazioni (2.23) e (2.24) contengono le concentrazioni superficiali $C^\circ_{Ox}$ e $C^\circ_{Red}$. In realta' abbiamo fin qui considerato il solo processo di trasferimento di massa dei reagenti e prodotti della reazione elettrodica dalla massa della soluzione alla superficie elettrodica e viceversa; nel prossimo paragrafo ricaveremo la dipendenza della velocita' del trasferimento elettronico dal potenziale: come si vedra', anche in tale relazione compaiono le concentrazioni superficiali delle specie partecipanti alla reazione elettrodica e cio' dara' il modo di eliminarle dalla relazione finale sfruttando i risultati qui ottenuti. Per il momento resta da sottolineare che gli effetti del trasporto di massa sono contenuti nei due parametri $i_{l,C}$ ed $i_{l,A}$. Le correnti limite dipendono a loro volta dalle concentrazioni massive e dai coefficienti di trasferimento di massa $m_{Ox}$ ed $m_{Red}$ (equazioni (2.21)-(2.22)) . Questi ultimi, infine, sono una misura della velocita' del trasferimento di massa (equazioni (2.18)-(2.19)) e dipendono da una serie di variabili sperimentali, quali l'agitazione della soluzione, la temperatura, il peso molecolare e la carica ionica (ad esempio, in una soluzione agitata e riscaldata il trasporto di massa e' molto piu' veloce).

Il trasferimento elettronico eterogeneo

In questo paragrafo ci occuperemo dello stadio piu' propriamente ``chimico'' che costituisce il processo elettrodico globale e cioe' la reazione superficiale di trasferimento elettronico (figura 2.2).

La reazione di riduzione:

$$Ox+ne^-\stackrel{k_C}{\rightarrow }Red$$

procede ad una velocita' $v_C$ proporzionale alla concentrazione superficiale di specie $Ox$ secondo:

$$v_C=k_CC^\circ_{Ox}$$

A tale reazione e' dunque associata una corrente catodica $i_C$ data da:

$$i_C=nFAv_C=nFAk_CC^\circ_{Ox}$$ (2.25)

In modo analogo, per la reazione di ossidazione:

$$Red\stackrel{k_A}{\rightarrow }Ox+ne^-$$

varra':

$$i_A=nFAv_A=nFAk_AC^\circ_{Red}$$ (2.26)

La velocita' netta della reazione di trasferimento elettronico e' data da:

$$v_{ct}=v_C-v_A$$ (2.27)

In condizioni stazionarie si ha dunque (equazione (2.17)):

$$i=i_C-i_A=nFAv_{ct}=nFA\left(k_CC^\circ_{Ox}-k_AC^\circ_{Red}\right)$$ (2.28)

(si ricordi la convenzione per cui una corrente netta catodica e' positiva).

Siccome la reazione di riduzione e quella di ossidazione avvengono all'interfaccia fra l'elettrodo e la soluzione, e' logico aspettarsi che le loro costanti di velocita' dipendano pesantemente dalla differenza di potenziale esistente attraverso tale interfaccia (ricordiamo che la differenza di potenziale in questione non e' altro che il potenziale elettrodico $E$, p.). Si trova in effetti che $k_C$ e $k_A$ dipendono esponenzialmente dal potenziale elettrodico secondo:

$$k_C = k_0\exp\left(-\alpha nf\left(E-E^\circ_{Ox/Red}\right)\right)$$ (2.29)

$$k_A = k_0\exp\left(\left(1-\alpha\right) nf\left(E-E^\circ_{Ox/Red}\right)\right)$$ (2.30)

dove $f=F/RT$ e $k_0$ e $\alpha$ sono parametri chiamati rispettivamente costante di velocita' standard e coefficiente di trasferimento. $\alpha$ e' quasi sempre compreso fra 0 e 1.

Quando $E=E^\circ_{Ox/Red}$, la reazione di riduzione e quella di ossidazione hanno il medesimo valore della costante di velocita', cioe' $k_0$. La costante di velocita' standard da' quindi una misura della mobilita' dell'equilibrio di scambio elettronico. Valori di $E$ diversi da $E^\circ_{Ox/Red}$ esaltano una delle due costanti e deprimono l'altra. Com'e' logico aspettarsi, valori di $E$ maggiori di $E^\circ_{Ox/Red}$ esaltano $k_A$ e deprimono $k_C$, cioe' accelerano l'ossidazione e rallentano la riduzione. Il viceversa avviene quando $E<E^\circ_{Ox/Red}$.

Il coefficiente di trasferimento $\alpha$ governa la simmetria della dipendenza di $k_C$ e $k_A$ da $E$ (percio' viene anche detto coefficiente di simmetria). Tanto per esemplificare, se $\alpha=0.5$, allora il valore di $k_C$ per $E=\left(E^\circ_{Ox/Red}-0.3\right)$ e' uguale a quello di $k_A$ per $E=\left(E^\circ_{Ox/Red}+0.3\right)$. D'altro canto, se $\alpha$ e' molto diverso da $0.5$ ( $\alpha\rightarrow 0$ oppure $\alpha\rightarrow 1$) l'effetto su $k_A$ dovuto ad un incremento di $E$ e' molto diverso da quello su $k_C$ causato da un decremento di $E$ di pari entita'.

Sostituendo le equazioni (2.29) e (2.30) nell'equazione (2.28) si ottiene:

$$i = nFAk_0\left[C^\circ_{Ox}\exp\left(-\alpha nf\left(E-E^\circ_{Ox/Red}\right)\right)\right.$$

$$\left.-C^\circ_{Red}\exp\left(\left(1-\alpha\right) nf\left(E-E^\circ_{Ox/Red}\right)\right)\right]$$ (2.31)

L'equazione (2.31) esprime la dipendenza della corrente dal potenziale elettrodico per effetto delle reazioni di trasferimento elettronico; il suo esame mostra che la corrente netta osservabile e' data dalla somma di due correnti ``parziali'' in direzioni opposte: una corrente catodica positiva e una corrente anodica negativa.

Come accennato nella sezione precedente, si vede che anche l'equazione (2.31) contiene le concentrazioni superficiali delle specie implicate nel processo elettrodico. Tali concentrazioni sono quanto meno difficili da misurare sperimentalmente. Per questo motivo vogliamo ora eliminarle dalla relazione finale. Cio' si realizza combinando l'equazione (2.31) con le equazioni (2.23) e (2.24) ricavate in precedenza. Tuttavia, prima di procedere, e' opportuno porre l'equazione (2.31) in una forma leggermente diversa.

Osserviamo innanzitutto che qualsiasi formulazione cinetica deve ridursi ad un'espressione di tipo termodinamico nel limite di condizioni di equilibrio. L'espressione (2.31) soddisfa tale requisito. Infatti, se l'interfaccia elettrodica si trova in condizioni di equilibrio, allora deve essere $E=E_{eq},\;i=0,\;C^\circ_{Ox}=C^*_{Ox},\;C^\circ_{Red}=C^*_{Red}$ ed e' facile verificare che la (2.31) si riduce alla legge di Nernst (2.3) o (2.4). In condizioni di equilibrio la corrente catodica $i_C$ e quella anodica $i_A$ sono uguali. Si puo' pertanto definire la cosiddetta corrente di scambio $i_0$ come il valore comune di $i_C$ ed $i_A$ in condizioni di equilibrio:

$$i_0 = nFAk_0C^*_{Ox}\exp\left(-\alpha nf\left(E_{eq}-E^\circ_{Ox/Red}\right)\right)$$ (2.32)

$$= nFAk_0C^*_{Red}\exp\left(\left(1-\alpha\right) nf\left(E_{eq}-E^\circ_{Ox/Red}\right)\right)$$ (2.33)

Combinando le equazioni (2.32) e (2.33) con l'equazione (2.31) e ricordando la definizione di sovratensione ($\eta=E-E_{eq}$), si ottiene:

$$i=i_0\left[\frac{C^\circ_{Ox}}{C^*_{Ox}}\exp\left(-\alpha nf... ...C^*_{Red}}\exp\left(\left(1-\alpha\right) nf\eta\right)\right]$$ (2.34)

Prima di procedere e' ancora opportuna una considerazione sul significato della corrente di scambio.

Dalla relazione di Nernst si ricava:

$$\exp\left(-\alpha nf\left(E_{eq}-E^\circ_{Ox/Red}\right)\right) = \left(\frac{C^*_{Ox}}{C^*_{Red}}\right)^{-\alpha}$$ (2.35)

$$\exp\left(\left(1-\alpha\right) nf\left(E_{eq}-E^\circ_{Ox/Red}\right)\right) = \left(\frac{C^*_{Ox}}{C^*_{Red}}\right)^{1-\alpha}$$ (2.36)

Sostituendo l'equazione (2.35) nella (2.32) oppure l'equazione (2.36) nella (2.33) si ottiene il medesimo risultato, ovvero:

$$i_0=nFAk_0{C^*_{Ox}}^{1-\alpha}{C^*_{Red}}^\alpha$$ (2.37)

Si vede quindi che $i_0$ e' in relazione diretta con $k_0$ . Il suo significato e' perfettamente analogo: quando il sistema elettrodico si trova all'equilibrio la corrente netta e' nulla, ma la reazione di riduzione e quella di ossidazione procedono entrambe generando due correnti ``parziali'' ($i_A$ e $i_C$) di uguale intensita', ma di verso opposto. $i_0$ e' per l'appunto il valore comune dell'intensita' di queste due correnti parziali e quindi misura la mobilita' dell'equilibrio redox eterogeneo. Valori elevati di $i_0$ indicano una reazione di trasferimento elettronico caratterizzata da una bassa energia di attivazione; viceversa, valori di $i_0$ molto bassi sono il risultato di una elevata energia di attivazione per il trasferimento elettronico eterogeneo.

L'espressione completa $i-\eta$

Come accennato nella sezione precedente, possiamo a questo punto combinare gli effetti del trasporto di massa e quelli della cinetica del trasferimento elettronico in un'unica relazione.

Grazie all'ipotesi di stazionarieta' della corrente (eq. (2.17)), le equazioni (2.23), (2.24) e (2.34) sono contemporaneamente valide. Possono quindi essere combinate eliminando le concentrazioni superficiali:

$$i=\frac{\exp\left(-\alpha nf\eta\right)-\exp\left(\left(1-\a... ...-\frac{\exp\left(\left(1-\alpha\right)nf\eta\right)}{i_{l,A}}}$$ (2.38)

L'equazione (2.38) rappresenta la dipendenza della corrente dalla sovratensione e fornisce la risposta alla domanda che ci eravamo posti a p..

Data una coppia redox $Ox/Red$ in soluzione, i valori di $E^\circ_{Ox/Red}$,$n$,$C^*_{Ox}$, $C^*_{Red}$,$m_{Ox}$,$m_{Red}$,$k_0$ e $\alpha$ rimangono determinati. Da questi valori derivano quelli di $i_0,i_{l,C}\ \mbox{e}\ i_{l,A}$. A questo punto, per ogni valore di sovratensione $\eta$, l'equazione (2.38) fornisce la corrente dovuta alla riduzione netta $Ox+ne^-\rightleftharpoons Red$ ($\eta<0$) o all'ossidazione netta $Red\rightleftharpoons Ox+ne^-$ ($\eta>0$).

L'andamento tipico della funzione $i(\eta)$ (detta anche caratteristica $i-\eta$) e' mostrato nella figura 2.3.

Figura 2.3: Caratteristica $i-\eta$. Nella costruzione del grafico si sono assunti i seguenti valori dei parametri: $n=1,\alpha=0.5,f=38.92\;V^{-1},i_0=1\times 10^{-5}\;\mu{A},i_{l,C}=0.9\;\mu{A},i_{l,A}=-0.7\;\mu{A}$

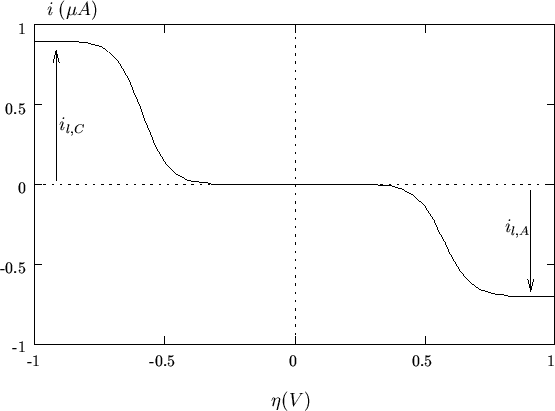Come si puo' vedere, la funzione presenta un ramo catodico positivo per valori di $\eta$ negativi e un ramo anodico negativo per valori di $\eta$ positivi. Per $\eta=0$ , cioe' all'equilibrio, si ha: $i=0$, come deve essere.

Man mano che il potenziale elettrodico si discosta dal valore di equilibrio ( $\eta>0\ \mbox{oppure}\ \eta<0$) la corrente che attraversa l'interfaccia cresce in modulo (il segno dipende da quello di $\eta$ , come abbiamo gia' sottolineato piu' volte).

Date le condizioni di stazionarieta' che abbiamo assunto, il valore di corrente corrispondente ad ogni valore di sovratensione e' una misura della velocita' (comune) a cui avvengono il trasporto di massa e la reazione elettrodica (eq. (2.17)). Tale velocita' sara' quella dello stadio limitante il processo globale. Un'analisi dell'eq. (2.34) mostra che la velocita' del trasferimento elettronico eterogeneo cresce esponenzialmente (in modulo) all'aumentare del modulo di $\eta$; d'altro canto, da quanto detto nella sezione (2.2.2.1) si deduce che la velocita' del trasporto di massa non puo' crescere indefinitamente, ma raggiunge un plateau determinato dalle correnti limite ($i_{l,C}$ per un processo netto di riduzione, $i_{l,A}$ per una ossidazione). Cio' ci consente di discutere sommariamente l'andamento della caratteristica $i-\eta$. Consideriamo per semplicita' il solo ramo catodico (la discussione dell'andamento del ramo anodico e' ovviamente speculare). Per piccoli valori di $\vert\eta\vert$ la concentrazione superficiale di $Ox$, $C^\circ_{Ox}$, e' solo di poco diversa da quella massiva $C^*_{Ox}$: in tali condizioni la velocita' del trasporto di massa non ha raggiunto ancora il suo valore massimo e il processo limitante risulta essere quello del trasferimento elettronico. Corrispondentemente, l'andamento della caratteristica $i-\eta$ e' di tipo esponenziale, simile a quello dell'eq. (2.34). Man mano che $\vert\eta\vert$ cresce, $C^\circ_{Ox}$ diminuisce finche' raggiunge un valore prossimo a $0$: a questo punto la velocita' del trasporto di massa ha raggiunto il suo massimo valore possibile e un ulteriore diminuzione di $\eta$ non puo' portare ad un incremento della corrente di riduzione. La caratteristica $i-\eta$ si appiattisce cosi' su un asintoto orizzontale e a questo punto l'intero processo e' limitato dal trasporto di massa.

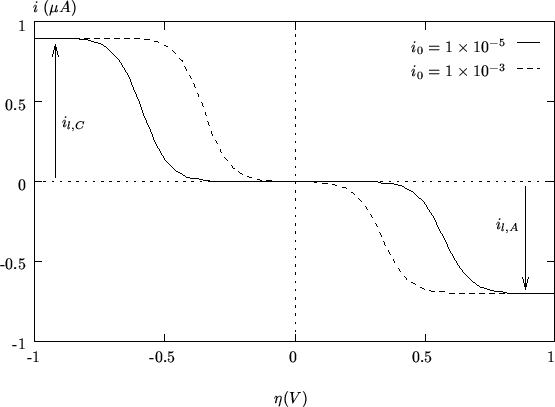
La velocita' dell' equilibrio di trasferimento elettronico, rappresentata, come si e' detto, dal parametro $i_0$, si riflette sull'appiattimento della caratterisctica $i-\eta$ in un intorno dell'origine (figura 2.4): in pratica' piu' la reazione redox eterogenea e' lenta e maggiore deve essere la sovratensione necessaria al passaggio di una determinata corrente; in altre parole, un'elevata energia di attivazione per lo stadio di trasferimento elettronico eterogeneo produce uno spostamento del ramo catodico a sovratensioni minori e di quello anodico a sovratensioni maggiori.

Figura 2.4: Dipendenza della caratteristica $i-\eta$ dalla corrente di scambio $i_0$. Nel grafico si sono assunti i seguenti valori dei parametri: $n=1,\alpha=0.5,f=38.92\;V^{-1},i_0=1\times 10^{-5}\;\mu{A},i_{l,C}=0.9\;\mu{A},i_{l,A}=-0.7\;\mu{A}$

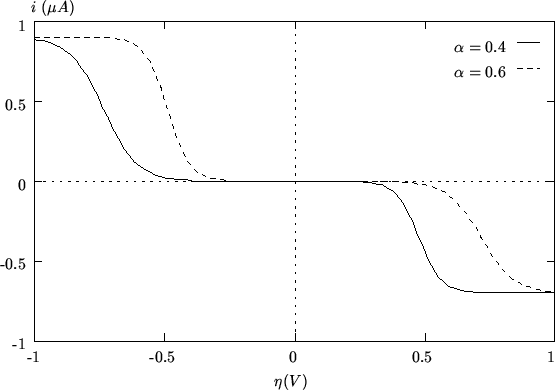
La simmetria della curva e' governata dal fattore di simmetria $\alpha$: la sua influenza, a parita' del resto, e' illustrata nella figura 2.5.

Figura 2.5: Dipendenza della caratteristica $i-\eta$ dal fattore di simmetria $\alpha$. Nella costruzione del grafico si sono assunti i seguenti valori dei parametri: $n=1,\alpha=0.5,f=38.92\;V^{-1},i_0=1\times 10^{-5}\;\mu{A},i_{l,C}=0.9\;\mu{A},i_{l,A}=-0.7\;\mu{A}$

Sovratensione di attivazione e sovratensione di concentrazione

La relazione  (2.38) puo' essere scritta in una forma semplificata che evidenzia in modo piu' diretto il contributo dovuto al trasporto di massa (contenuto nei parametri $i_{l,C}$ e $i_{l,A}$) e quello dovuto alla cinetica del trasferimento elettronico (contenuto essenzialmente nel parametro $i_0$).

Per valori di $\vert\eta\vert$ sufficientemente piccoli, gli esponenziali al numeratore nell'equazione (2.38) possono essere approssimati con le rispettive serie di Taylor troncate al termine lineare:

$$\begin{eqnarray*} \exp\left(-\alpha nf\eta\right)&\approx&1-\alpha nf\eta\\ \ex... ...a\right) nf\eta\right)&\approx&1+\left(1-\alpha\right) nf\eta\\ \end{eqnarray*}$$

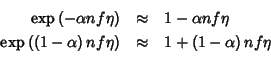
Sostituendo nell'equazione (2.38), restringendosi a valori di $\eta$ tali che $nf\eta\approx0$ e riarrangiando si ottiene:

$$\eta=-\frac{1}{nf}\left(\frac{1}{i_0}+\frac{1}{i_{l,C}}-\frac{1}{i_{l,A}}\right)i$$ (2.39)

L'equazione (2.39) e' formalmente identica alla legge di Ohm in cui i termini in parentesi giocano il ruolo di resistenze. Definendo:

$$\begin{eqnarray*} R_{ct}&=&\frac{1}{nfi_0}\\ R_{mt}&=&\frac{1}{nf}\left(\frac{1}{i_{l,C}}-\frac{1}{i_{l,A}}\right)\\ \end{eqnarray*}$$

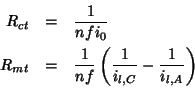
si ha:

$$\eta = -\left(R_{ct}+R_{mt}\right)i$$

$$= -R_{ct}i-R_{mt}i$$

$$= \eta_{ct}+\eta_{mt}$$ (2.40)

Per ottenere passaggio di una determinata corrente attraverso un'interfaccia elettrodica, il potenziale di quest'ultima deve essere aumentato (per una corrente netta anodica) o diminuito (per una corrente netta catodica) rispetto al valore di equilibrio di una quantita' $\eta$. In generale, per un valore fissato di corrente, $\eta$ e' tanto maggiore quanto minori sono i parametri caratteristici $i_0$, $i_{l,C}$ ed $i_{l,A}$. Dalla relazione (2.40) si vede che $\eta$ e' esprimibile come somma di due contributi: il termine $\eta_{ct}$, detto sovratensione di attivazione, e' necessario a vincere la barriera di attivazione che si oppone al trasferimento elettronico eterogeneo; il termine $\eta_{mt}$, detto sovratensione di concentrazione, e' necessario a vincere la lentezza del movimento delle specie attive dalla soluzione alla superficie elettrodica e viceversa.

I due contributi alla sovratensione $\eta$ possono avere peso simile oppure uno puo' essere nettamente prevalente sull'altro. Cosi', ad esempio, se una coppia redox e' caratterizzata da una corrente di scambio $i_0$ molto piu' grande delle correnti limite $i_{l,C}$ ed $i_{l,A}$, si avra': $R_{ct}\ll R_{mt}$ e quindi: $\eta\approx\eta_{mt}$: cioe' la quasi totalita' della sovratensione da fornire per ottenere una certa corrente viene impiegata per forzare il movimento delle specie attive nella soluzione, mentre una volta che queste giungono alla superficie elettrodica scambiano gli elettroni molto rapidamente.

Considerazioni riassuntive sulla relazione fra corrente e differenza di potenziale applicata

Le considerazioni svolte nella sezione (2.2.2) sono del tutto generali e si applicano sia al catodo che all'anodo della cella di elettrolisi. La coppia $Ox_C/Red_C$ che reagisce al catodo sara' caratterizzata da una certa caratteristica $i-\eta$: il termine $\left(\eta_C\right)_i$ che compare nell'equazione (2.12) e' ricavabile dal ramo catodico di tale curva (si noti che cio' richiede la conoscenza dei parametri $i_0$, $\alpha$, $i_{l,C}$ ed $i_{l,A}$ per la coppia $Ox_C/Red_C$). Analogamente, la coppia $Ox_A/Red_A$ che reagisce all'anodo avra' una caratteristica $i-\eta$ dal ramo anodico della quale e' possibile (conoscendo i parametri necessari) ricavare il termine $\left(\eta_a\right)_i$ che compare nell'equazione (2.12). Un'esemplificazione di quanto detto e' mostrata nella figura 2.6

Figura 2.6: Date le due coppie redox $Ox_C/Red_C$ e $Ox_A/Red_A$, caratterizzate dalle curve $i-\eta$ indicate, la sovratensione corrispondente ad una corrente di $0.5\;\mu A$ e' data da un contributo catodico della coppia $Ox_C/Red_C$ e da un contributo anodico della coppia $Ox_A/Red_A$.

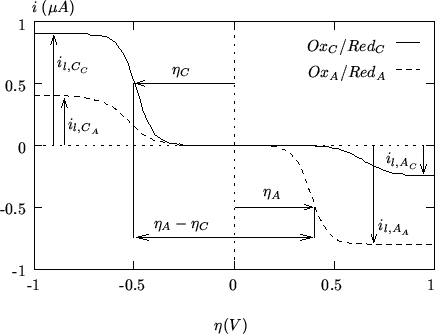Possiamo a questo punto riassumere quanto detto sulla relazione fra corrente di elettrolisi e differenza di potenziale applicata.

La differenza di potenziale che bisogna applicare per ottenere una corrente $i$ e' esprimibile come somma di vari contributi (equazione (2.12)):

• il primo contributo e' imposto dalla termodinamica ed e' pari alla differenza di potenziale esistente fra anodo e catodo a circuito aperto. Tale termine si puo' calcolare dalla legge di Nernst (equazioni (2.3) e (2.4))

• il secondo contributo e' la sovratensione, che comprende cumulativamente la sovratensione anodica e quella catodica (si veda la figura 2.6). Il termine di sovratensione e' necessario per vincere le barriere di attivazione associate a ciascuno dei due processi elettrodici: come accennato nella sezione (2.2.2.4), tali barriere di attivazione possono essere originate, almeno nel caso piu' semplice, da una lentezza del trasporto di massa (sovratensione di concentrazione) e/o da una lentezza del trasferimento elettronico eterogeneo (sovratensione di attivazione)

• il terzo contributo alla differenza di potenziale e' la caduta ohmica, che trae origine dalla resistenza della soluzione al passaggio di corrente

La sovratensione e la caduta ohmica dipendono dalla corrente crescendo al crescere di essa. Questo comporta che, com'e' ovvio aspettarsi, per ottenere correnti maggiori bisogna aumentare la differenza di potenziale applicata agli elettrodi.