Si e' appena visto che la conducibilita' specifica ![]() dipende (a
parita' delle altre condizioni) dalla carica degli ioni presenti in
soluzione. Questo rende
dipende (a
parita' delle altre condizioni) dalla carica degli ioni presenti in
soluzione. Questo rende ![]() inadatta al confronto fra elettroliti
diversi.
inadatta al confronto fra elettroliti
diversi.
Si definisce percio' la conducibilita' equivalente ![]() ,
normalizzando
,
normalizzando ![]() rispetto alla concentrazione totale di cariche
di un dato segno (ovviamente, in una soluzione la concentrazione
totale di cariche positive e' sempre uguale alla concentrazione totale
di cariche negative).
rispetto alla concentrazione totale di cariche
di un dato segno (ovviamente, in una soluzione la concentrazione
totale di cariche positive e' sempre uguale alla concentrazione totale
di cariche negative).
Nel caso in cui la soluzione contenga un solo elettrolita disciolto, la concentrazione totale di cariche di un dato segno coincide con la normalita' dell'elettrolita, ovvero con la normalita' di ciascuno degli ioni che costituiscono l'elettrolita.
Il ``grammo equivalente'' (o semplicemente ``equivalente'') e' definito, in rapporto ad una particolare reazione, come la frazione di mole di una certa specie chimica (molecola o ione) richiesta dalla stechiometria della reazione, quando i coefficienti stechiometrici di reagenti e prodotti vengano ridotti a numeri minori o uguali ad 1 dividendoli per il loro minimo comune multiplo.
Cosi', ad esempio, nella reazione di dissociazione di ![]() :
:
si ha:
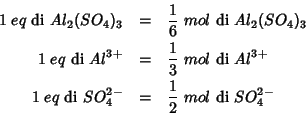
e quindi, indicando con ![]() la normalita' e con
la normalita' e con ![]() la molarita' formale:
la molarita' formale:
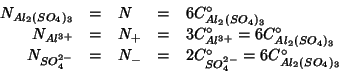
da cui si vede che: ![]() .
.
Se ![]() e' espressa in
e' espressa in ![]() ed
ed ![]() in
in ![]() , allora la
conducibilita' equivalente per una soluzione contenente un solo elettrolita, espressa in
, allora la
conducibilita' equivalente per una soluzione contenente un solo elettrolita, espressa in ![]() e' definita da:
e' definita da:
Per una soluzione contenente piu' di un elettrolita, la conducibilita' equivalente si ottiene sommando i contributi dovuti a ciascun elettrolita:
Se e' vero che la conducibilita' equivalente elimina l'effetto dovuto alla carica ionica, essa continua a dipendere dalla concentrazione, essendo generalmente una sua funzione decrescente. Cio' e' dovuto in primo luogo al fatto che all'aumentare della concentrazione aumentano le forze di interazione ione-ione, che diminuiscono la velocita' di migrazione degli ioni. Per gli elettroliti deboli c'e' un secondo effetto connesso al grado di dissociazione, che diminuisce all'aumentare della concentrazione. Ad esempio, per la reazione di ionizzazione:
detti ![]() il grado di dissociazione,
il grado di dissociazione, ![]() la costante di
equilibrio e
la costante di
equilibrio e ![]() la concentrazione formale della specie
la concentrazione formale della specie ![]() , si
verifica facilmente che (per valori sufficientemente piccoli del grado
di dissociazione) vale:
, si
verifica facilmente che (per valori sufficientemente piccoli del grado
di dissociazione) vale:
Cio' fa si' che per concentrazioni non molto piccole, la conducibilita' equivalente di un elettrolita forte sia generalmente maggiore di quella di un elettrolita debole.
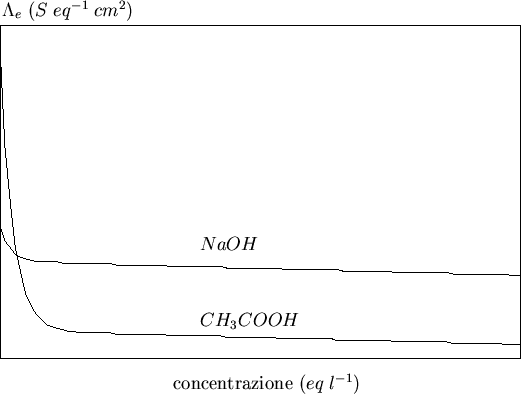
Per concentrazioni via via minori, la conducibilita' equivalente tende ad aumentare perche' diminuiscono le interazioni ``rallentanti'' fra gli ioni. Per gli elettroliti deboli, come appena detto, la diminuzione di concentrazione causa un aumento di conducibilita' equivalente anche in virtu' di un aumento del grado di dissociazione.
Alla luce di quanto appena visto, possiamo dire che la relazione
funzionale che lega la conducibilita' specifica alla concentrazione e'
del tipo:
![]() , dove
, dove ![]() include gli effetti non
lineari dovuti alle interazioni inter-ioniche e al grado di
dissociazione; nella conducibilita' equivalente:
include gli effetti non
lineari dovuti alle interazioni inter-ioniche e al grado di
dissociazione; nella conducibilita' equivalente:
In tutti i casi, al diminuire della concentrazione la conducibilita'
equivalente tende ad un valore limite ![]() detto
conducibilita' equivalente a diluizione infinita
(figura 3.2).
detto
conducibilita' equivalente a diluizione infinita
(figura 3.2).
 |
Diversamente da ![]() ,
, ![]() non dipende dalle forze
inter-ioniche (perche' in condizioni di diluizione infinita ciascuno
ione ignora la presenza degli altri ioni e ``vede'' solo molecole di
solvente) ne' dal fatto che l'elettrolita sia forte o debole (in
condizioni di diluizione infinita si ha
non dipende dalle forze
inter-ioniche (perche' in condizioni di diluizione infinita ciascuno
ione ignora la presenza degli altri ioni e ``vede'' solo molecole di
solvente) ne' dal fatto che l'elettrolita sia forte o debole (in
condizioni di diluizione infinita si ha ![]() ). A tale proposito
si puo' osservare come, ad esempio, sia
). A tale proposito
si puo' osservare come, ad esempio, sia
![]() .
.
Dato che la conducibilita' equivalente a diluizione infinita dipende solamente dalle caratteristiche del catione e dell'anione di cui e' composto un elettrolita (e dalle loro interazioni con il solvente) non stupisce che per essa esista una relazione di addittivita' nota come legge di Kohlrausch:
Nell'espressione su scritta, ![]() e' la conducibilita'
equivalente a diluizione infinita del catione e
e' la conducibilita'
equivalente a diluizione infinita del catione e ![]() quella
dell'anione di un elettrolita. Queste due grandezze sono
sperimentalmente accessibili ed esistono tabelle molto estese in base
alle quali e' possibile ricavare la conducibilita' equivalente a
diluizione infinita per un gran numero di elettroliti (tabella
3.1).
quella
dell'anione di un elettrolita. Queste due grandezze sono
sperimentalmente accessibili ed esistono tabelle molto estese in base
alle quali e' possibile ricavare la conducibilita' equivalente a
diluizione infinita per un gran numero di elettroliti (tabella
3.1).
| Cationi | Anioni | ||
| 350 | 198.6 | ||
| 77.5 |
|
110.5 | |
| 76.8 |
|
101.0 | |
| 73.5 | 80 | ||
| 73.5 | 78.1 | ||
| 70.0 | 76.8 | ||
| 69.5 | 76.3 | ||
| 63.6 | 71.4 | ||
| 63.0 | 69.3 | ||
| 61.9 | 67.3 | ||
| 59 | 55.7 | ||
| 55 | 55.4 | ||
| 53.6 | 54.5 | ||
| 54.0 | 40 9 | ||
| 53.1 | 40.5 | ||
| 53.1 | 40.2 | ||
|
|
51.8 | butirrato | 32.6 |
| 50.1 | 32.4 | ||
|
|
47.2 | picrato | 30.4 |
Per una soluzione contenente piu' di due specie ioniche, la legge di Kohlrausch assume la forma seguente:
dove la sommatoria e' estesa a tutte le specie ioniche presenti nella soluzione. Si puo' osservare che una relazione simile e' approssimativamente valida anche a diluizione finita e cio' costituisce la base concettuale per le titolazioni conduttimetriche (sezione (3.4.2)).
Notiamo ancora che la maggior parte degli ioni possiede valori di
![]() molto simili (tabella 3.1). Fanno
eccezione gli ioni
molto simili (tabella 3.1). Fanno
eccezione gli ioni ![]() ed
ed ![]() , che hanno conducibilita'
equivalenti a diluizione infinita molto maggiori. Cio' viene
generalmente attribuito al particolare meccanismo di migrazione. Ad
esempio, per lo ione
, che hanno conducibilita'
equivalenti a diluizione infinita molto maggiori. Cio' viene
generalmente attribuito al particolare meccanismo di migrazione. Ad
esempio, per lo ione ![]() si ha una sorta di ``staffetta'',
illustrata in figura 3.3.
si ha una sorta di ``staffetta'',
illustrata in figura 3.3.
Limitatamente agli elettroliti forti, esiste una relazione che lega la
conducibilita' equivalente ad una certa concentrazione (![]() )
alla conducibilita' equivalente a diluizione infinita
)
alla conducibilita' equivalente a diluizione infinita ![]() :
:
(![]() e
e ![]() sono parametri che tengono conto degli effetti dovuti
alle interazioni inter-ioniche che si instaurano a diluizione finita)
sono parametri che tengono conto degli effetti dovuti
alle interazioni inter-ioniche che si instaurano a diluizione finita)
Questa relazione, dovuta ad Onsager, viene spesso usata per ricavare
![]() estrapolando misure di conducibilita' equivalente a
diverse normalita'.
estrapolando misure di conducibilita' equivalente a
diverse normalita'.