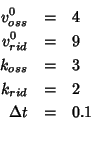66. In questa sezione useremo un semplicissimo modello matematico della reazione elettrodica per comprendere piu' a fondo il modo in cui un sistema elettrodico raggiunge l'equilibrio e come in tale stato di equilibrio esista una differenza di potenziale fra metallo e soluzione.
Sappiamo che la semireazione redox che interconverte i due membri della coppia redox presente nel sistema elettrodico e' la ``risultante'' di due processi che sono uno l'inverso dell'altro: l'ossidazione e la riduzione.
Indichiamo con ![]() e
e ![]() le velocita' di questi due
processi. Se consideriamo il semplice sistema
le velocita' di questi due
processi. Se consideriamo il semplice sistema ![]() , allora
, allora
![]() e' il numero di moli di atomi di
e' il numero di moli di atomi di ![]() che abbandonano il
metallo per andare in soluzione come ioni
che abbandonano il
metallo per andare in soluzione come ioni ![]() nell'unita' di
tempo. Analogamente,
nell'unita' di
tempo. Analogamente, ![]() rappresenta il numero di moli di ioni
rappresenta il numero di moli di ioni
![]() che si depositano dalla soluzione sul filo metallico
nell'unita' di tempo.
che si depositano dalla soluzione sul filo metallico
nell'unita' di tempo.
Se in automobile stiamo viaggiando ad una velocita' ![]() , in un
intervallo di tempo
, in un
intervallo di tempo ![]() percorreremo uno spazio pari
percorreremo uno spazio pari
![]() . In modo identico, il numero di moli di atomi di
. In modo identico, il numero di moli di atomi di
![]() che abbandonano il metallo e il numero di moli di ioni
che abbandonano il metallo e il numero di moli di ioni ![]() che vi si depositano in un intervallo di tempo
che vi si depositano in un intervallo di tempo ![]() sono
dati, rispettivamente, da
sono
dati, rispettivamente, da
![]() e
e
![]() .
.
Il punto essenziale per cui il sistema elettrodico raggiunge
l'equilibrio e' che ![]() e
e ![]() cambiano nel
tempo a causa della separazione di carica che si instaura fra metallo
e soluzione.
cambiano nel
tempo a causa della separazione di carica che si instaura fra metallo
e soluzione.
La dipendenza delle velocita' dei due processi (ossidazione e riduzione) dalla separazione di carica fra metallo e soluzione puo' essere espressa in modo molto semplice come segue:
Nelle due espressioni su scritte, ![]() e
e ![]() sono delle
costanti positive e
sono delle
costanti positive e ![]() e' la carica elettrica in eccesso presente
sul metallo (chiaramente, ad ogni istante di tempo, la carica
e' la carica elettrica in eccesso presente
sul metallo (chiaramente, ad ogni istante di tempo, la carica ![]() sul metallo e' bilanciata da una carica di uguale entita' ma di segno
opposto presente in soluzione). Inizialmente, a
sul metallo e' bilanciata da una carica di uguale entita' ma di segno
opposto presente in soluzione). Inizialmente, a ![]() , non c'e'
separazione di carica fra metallo e soluzione; in tale condizione si
ha
, non c'e'
separazione di carica fra metallo e soluzione; in tale condizione si
ha ![]() e quindi
e quindi
![]() e
e
![]() :
:
![]() e
e ![]() sono cioe' i valori iniziali di
sono cioe' i valori iniziali di
![]() e
e ![]() , rispettivamente. Col trascorrere del tempo,
sul metallo si accumula un eccesso di carica elettrica: se
, rispettivamente. Col trascorrere del tempo,
sul metallo si accumula un eccesso di carica elettrica: se ![]() ,
allora
,
allora ![]() viene aumentata di
viene aumentata di ![]() rispetto al suo
valore iniziale e
rispetto al suo
valore iniziale e ![]() viene diminuita di
viene diminuita di ![]() rispetto al suo valore iniziale; si ha il viceversa, se
rispetto al suo valore iniziale; si ha il viceversa, se ![]() . Le
due espressioni dicono quindi matematicamente cio' che abbiamo gia'
illustrato a parole (punto 9): un eccesso di carica
elettrica positiva sul metallo accelera l'ossidazione e
rallenta la riduzione; il viceversa vale se sul metallo e'
presente un eccesso di carica negativa. Le costanti moltiplicative
. Le
due espressioni dicono quindi matematicamente cio' che abbiamo gia'
illustrato a parole (punto 9): un eccesso di carica
elettrica positiva sul metallo accelera l'ossidazione e
rallenta la riduzione; il viceversa vale se sul metallo e'
presente un eccesso di carica negativa. Le costanti moltiplicative
![]() e
e ![]() esprimono la sensibilita' di ciascuna
velocita' ad un determinato eccesso di carica sul metallo: maggiore e'
il loro valore, e maggiore sara' l'effetto di accelerazione o
rallentamento sulla corrispondente velocita' per un dato valore di
esprimono la sensibilita' di ciascuna
velocita' ad un determinato eccesso di carica sul metallo: maggiore e'
il loro valore, e maggiore sara' l'effetto di accelerazione o
rallentamento sulla corrispondente velocita' per un dato valore di
![]() .
.
Chiaramente, le equazioni (A.1) e (A.2) sono ben lungi dal rappresentare anche solo lontanamente la complessita' di un sistema elettrodico (ad esempio, abbiamo volutamente tralasciato di rappresentare la dipendenza dalla concentrazione); cio' non di meno, esse possiedono le caratteristiche minime che servono ad illustrare l'evoluzione del sistema.
Assegniamo ora dei valori numerici ai vari parametri e proviamo a seguire l'evoluzione del sistema nel tempo.
Poniamo, ad esempio:
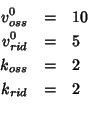
Questa scelta corrisponde alla situazione che abbiamo prima
descritto (punto 9), in cui a ![]() l'ossidazione e' piu'
veloce della riduzione.
l'ossidazione e' piu'
veloce della riduzione.
Per seguire l'evoluzione temporale del sistema elettrodico,
consideriamo un intervallo di tempo ![]() e calcoliamo i
valori che assumono
e calcoliamo i
valori che assumono ![]() ,
, ![]() e
e ![]() dopo un tempo
pari a
dopo un tempo
pari a ![]() ,
, ![]() ,
, ![]() ...
...
A ![]() , come abbiamo gia' visto, si ha:
, come abbiamo gia' visto, si ha:
![]() ,
,
![]() e
e ![]() .
.
Quando e' trascorso un tempo pari a ![]() , un numero di
moli di atomi di
, un numero di
moli di atomi di ![]() pari a
pari a
![]() hanno
abbandonato il metallo sotto forma di ioni
hanno
abbandonato il metallo sotto forma di ioni ![]() : per effetto
dell'ossidazione, quindi, sul metallo si e' creata una carica
negativa pari a
: per effetto
dell'ossidazione, quindi, sul metallo si e' creata una carica
negativa pari a ![]() mole di elettroni; chiamiamo
mole di elettroni; chiamiamo ![]() tale carica, per sottolineare che e' l'eccesso di carica dovuto al
solo processo di ossidazione. Nello stesso tempo, un numero di
moli di ioni
tale carica, per sottolineare che e' l'eccesso di carica dovuto al
solo processo di ossidazione. Nello stesso tempo, un numero di
moli di ioni ![]() dato da
dato da
![]() si e'
depositato sul metallo dalla soluzione: questo processo crea quindi
sul metallo una carica positiva
si e'
depositato sul metallo dalla soluzione: questo processo crea quindi
sul metallo una carica positiva ![]() . L'eccesso di
carica risultante sul metallo e' dato dalla somma algebrica di
. L'eccesso di
carica risultante sul metallo e' dato dalla somma algebrica di
![]() e
e ![]() , cioe':
, cioe':
![]() . Vediamo quindi che, siccome
abbiamo supposto che l'ossidazione sia inizialmente piu' veloce della
riduzione, sul metallo si accumula carica negativa (e nella soluzione
si crea una corrispondente carica positiva). La carica
. Vediamo quindi che, siccome
abbiamo supposto che l'ossidazione sia inizialmente piu' veloce della
riduzione, sul metallo si accumula carica negativa (e nella soluzione
si crea una corrispondente carica positiva). La carica ![]() accumulatasi sul metallo determina a sua volta un cambiamento di
accumulatasi sul metallo determina a sua volta un cambiamento di
![]() e
e ![]() secondo le equazioni (A.1)
e (A.2):
secondo le equazioni (A.1)
e (A.2):
![]() e
e
![]() . Troviamo cosi' che,
dopo un tempo pari a
. Troviamo cosi' che,
dopo un tempo pari a ![]() , il processo inizialmente piu'
veloce (l'ossidazione) e' rallentato, mentre quello piu' lento (la
riduzione) e' accelerato, come avevamo gia' detto in precedenza.
, il processo inizialmente piu'
veloce (l'ossidazione) e' rallentato, mentre quello piu' lento (la
riduzione) e' accelerato, come avevamo gia' detto in precedenza.
A questo punto siamo pronti per calcolare i valori di ![]() ,
,
![]() e
e ![]() dopo un tempo pari a
dopo un tempo pari a ![]() , a
partire dai valori che abbiamo appena calcolato al tempo
, a
partire dai valori che abbiamo appena calcolato al tempo
![]() . Durante questo secondo intervallo di tempo,
l'ossidazione produce sul metallo una carica negativa data da:
. Durante questo secondo intervallo di tempo,
l'ossidazione produce sul metallo una carica negativa data da:
![]() e la riduzione crea nel
filo metallico una carica positiva pari a
e la riduzione crea nel
filo metallico una carica positiva pari a
![]() . La carica risultante sul
metallo sara' data ora dalla somma algebrica di tre termini: la carica
che si era gia' accumulata durante il primo intervallo di tempo
(chiamiamola
. La carica risultante sul
metallo sara' data ora dalla somma algebrica di tre termini: la carica
che si era gia' accumulata durante il primo intervallo di tempo
(chiamiamola
![]() ), il contributo negativo
dell'ossidazione relativo al secondo intervallo di tempo e il
contributo positivo della riduzione nello stesso intervallo di
tempo. In simboli:
), il contributo negativo
dell'ossidazione relativo al secondo intervallo di tempo e il
contributo positivo della riduzione nello stesso intervallo di
tempo. In simboli:
![]() .
.
I valori di ![]() e
e ![]() al tempo
al tempo ![]() si
ricavano sempre dalle espressioni (A.1) e (A.2):
si
ricavano sempre dalle espressioni (A.1) e (A.2):
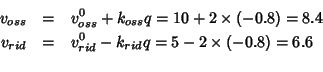
Come si vede, dopo un tempo pari a ![]() , sul filo di
, sul filo di ![]() continua ad accumularsi carica negativa; contemporaneamente,
continua ad accumularsi carica negativa; contemporaneamente,
![]() continua a diminuire e
continua a diminuire e ![]() continua ad aumentare.
continua ad aumentare.
Sulla base di quanto appena visto, possiamo ora generalizzare le
formule per il calcolo di ![]() ,
, ![]() e
e ![]() . A un dato
tempo, si calcolano
. A un dato
tempo, si calcolano ![]() e
e ![]() utilizzando i valori di
utilizzando i valori di
![]() e
e ![]() , rispettivamente, calcolati nello step
precedente. Poi si calcola
, rispettivamente, calcolati nello step
precedente. Poi si calcola ![]() sommando i valori correnti di
sommando i valori correnti di
![]() e
e ![]() e il valore di
e il valore di ![]() allo step
precedente. Infine, si aggiornano i valori di
allo step
precedente. Infine, si aggiornano i valori di ![]() e
e
![]() con il valore di
con il valore di ![]() appena ottenuto.
appena ottenuto.
Indicando con l'indice ![]() lo step ``corrente'', corrispondente
percio' al tempo
lo step ``corrente'', corrispondente
percio' al tempo ![]() , il calcolo puo' venire cosi'
illustrato:
, il calcolo puo' venire cosi'
illustrato:
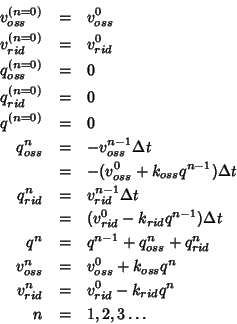
Con una calcolatrice da tavolo (piu' comodamente con un computer, se si conosce un linguaggio di programmazione qualsiasi) e' possibile costruire la tabella che segue:
Commentiamo i dati riportati nella tabella (per comodita', l'andamento
di ![]() ,
, ![]() e
e ![]() in funzione del tempo e' stato
diagrammato nelle figure (A.1) e (A.2)).
in funzione del tempo e' stato
diagrammato nelle figure (A.1) e (A.2)).
Siccome siamo nell'ipotesi che l'ossidazione sia inizialmente piu'
veloce della riduzione, nel periodo iniziale la carica negativa creata
dalla ossidazione sul metallo e' maggiore (in modulo) della carica
positiva prodotta dalla riduzione; cio' fa si' che il metallo acquisti
una carica netta negativa che cresce nel tempo (la colonna
![]() nella tabella e la figura (A.1)). Tuttavia, la
presenza di questa carica netta negativa sul filo di
nella tabella e la figura (A.1)). Tuttavia, la
presenza di questa carica netta negativa sul filo di ![]() provoca
una diminuzione di
provoca
una diminuzione di ![]() e un aumento di
e un aumento di ![]() ; la
conseguenza e' che il caricamento negativo del metallo rispetto alla
soluzione avviene a velocita' via via minore. Si arriva cosi',
inevitabilmente, al momento in cui, nell'intervallo
; la
conseguenza e' che il caricamento negativo del metallo rispetto alla
soluzione avviene a velocita' via via minore. Si arriva cosi',
inevitabilmente, al momento in cui, nell'intervallo ![]() , si
ha
, si
ha
![]() (step numero 16 nella tabella): da questo
punto in poi,
(step numero 16 nella tabella): da questo
punto in poi, ![]() ,
, ![]() e
e ![]() smettono di cambiare e
il sistema elettrodico ha raggiunto l'equilibrio.
smettono di cambiare e
il sistema elettrodico ha raggiunto l'equilibrio.
E' importante realizzare che, all'equilibrio, l'ossidazione e la
riduzione non si sono fermate: i due processi stanno continuando ad
avvenire, ma alla stessa velocita' (![]() (moli di
(moli di ![]() o
o
![]() )/(unita' di tempo), nella tabella).
)/(unita' di tempo), nella tabella).
Osserviamo ancora che, quando si e' raggiunto l'equilibrio, sul filo
di ![]() e' presente un eccesso di carica negativa pari a
e' presente un eccesso di carica negativa pari a ![]() moli di elettroni. Chiaramente la soluzione conterra' un eccesso di
carica positiva di uguale valore. A causa di questa separazione di
carica, fra metallo e soluzione esiste una differenza di potenziale
elettrico che abbiamo chiamato potenziale elettrodico.
moli di elettroni. Chiaramente la soluzione conterra' un eccesso di
carica positiva di uguale valore. A causa di questa separazione di
carica, fra metallo e soluzione esiste una differenza di potenziale
elettrico che abbiamo chiamato potenziale elettrodico.
Provate a ripetere i calcoli cambiando i parametri: ad esempio, costruite una tabella analoga per il caso in cui la riduzione sia inizialmente piu' veloce dell'ossidazione. Una scelta opportuna dei parametri potrebbe essere: