46. Da quanto detto al punto 45, ci aspettiamo che la conducibilita' sia approssimativamente proporzionale alla concentrazione ionica in soluzione.
Per evidenziare cio' possiamo tentativamente scrivere:
dove ![]() e' una costante e
e' una costante e ![]() e' la concentrazione
molare dell'elettrolita.
e' la concentrazione
molare dell'elettrolita.
La relazione su scritta fa prevedere che una soluzione ![]() di
di ![]() abbia una conducibilita' specifica doppia di una soluzione
abbia una conducibilita' specifica doppia di una soluzione
![]() dello stesso sale: effettivamente, cio' e' quanto piu'
o meno si verifica in pratica.
dello stesso sale: effettivamente, cio' e' quanto piu'
o meno si verifica in pratica.
Tuttavia, ci sono fondamentalmente due tipi di complicazioni per cui la relazione che abbiamo ottimisticamente scritto sopra va un po' modificata.
47.
La prima complicazione si evidenzia se confrontiamo
elettroliti diversi alla stessa concentrazione molare. Ad esempio, si
trova che una soluzione ![]() di
di ![]() ha una
conducibilita' circa doppia di una soluzione equimolare di
ha una
conducibilita' circa doppia di una soluzione equimolare di
![]() . Questo potrebbe essere spiegato semplicemente dicendo che la
costante di proporzionalita' per
. Questo potrebbe essere spiegato semplicemente dicendo che la
costante di proporzionalita' per ![]() e' doppia di quella
relativa a
e' doppia di quella
relativa a ![]() . In realta' il motivo e' un altro: la
conducibilita' e' legata alla corrente elettrica e quest'ultima e'
dovuta al flusso di cariche elettriche. Il fatto che le cariche
elettriche siano in realta' situate su degli ioni non ha alcuna
importanza. Lo ione
. In realta' il motivo e' un altro: la
conducibilita' e' legata alla corrente elettrica e quest'ultima e'
dovuta al flusso di cariche elettriche. Il fatto che le cariche
elettriche siano in realta' situate su degli ioni non ha alcuna
importanza. Lo ione ![]() ha una carica positiva doppia rispetto
allo ione
ha una carica positiva doppia rispetto
allo ione ![]() : se
: se ![]() ioni
ioni ![]() si spostano da un punto
all'altro della soluzione, cio' equivale ad una corrente elettrica di
si spostano da un punto
all'altro della soluzione, cio' equivale ad una corrente elettrica di
![]() cariche positive; se
cariche positive; se ![]() ioni
ioni ![]() fanno la stessa cosa,
la corrente sara' di sole
fanno la stessa cosa,
la corrente sara' di sole ![]() cariche positive. Lo stesso vale
ovviamente per gli ioni
cariche positive. Lo stesso vale
ovviamente per gli ioni ![]() e
e ![]() .
.
In altre parole, la concentrazione da cui dipende la conducibilita'
specifica di una soluzione non e' quella formale degli ioni, ma e'
piuttosto la concentrazione totale di cariche positive (o negative)
presenti nella soluzione: il fatto che queste cariche siano
``raggruppate'' a due a due (come nello ione ![]() ), a tre a tre
(come nello ione
), a tre a tre
(come nello ione ![]() ) o in qualsiasi altro modo non ha
importanza. La relazione fra conducibilita' specifica e
concentrazione va allora riscritta nel modo seguente:
) o in qualsiasi altro modo non ha
importanza. La relazione fra conducibilita' specifica e
concentrazione va allora riscritta nel modo seguente:
dove ![]() viene chiamata concentrazione equivalente
dell'elettrolita ed e' la concentrazione totale di cariche di un dato
segno (non importa specificare se positivo o negativo, visto che il
principio di conservazione della carica elettrica ci assicura che in
una soluzione la concentrazione totale di cariche positive e' sempre
uguale alla concentrazione totale di cariche negative). Ad esempio,
per una soluzione di
viene chiamata concentrazione equivalente
dell'elettrolita ed e' la concentrazione totale di cariche di un dato
segno (non importa specificare se positivo o negativo, visto che il
principio di conservazione della carica elettrica ci assicura che in
una soluzione la concentrazione totale di cariche positive e' sempre
uguale alla concentrazione totale di cariche negative). Ad esempio,
per una soluzione di ![]() ,
, ![]() coincide con la concentrazione
molare del sale; ma per una soluzione di
coincide con la concentrazione
molare del sale; ma per una soluzione di ![]() ,
, ![]() e' pari a
due volte la concentrazione molare del sale (se abbiamo sciolto
e' pari a
due volte la concentrazione molare del sale (se abbiamo sciolto
![]() fino ad avere una concentrazione molare di
fino ad avere una concentrazione molare di ![]() ,
la concentrazione di cariche positive (o negative, e' lo stesso) in
soluzione e' pari a
,
la concentrazione di cariche positive (o negative, e' lo stesso) in
soluzione e' pari a ![]() poiche' ogni ione
poiche' ogni ione ![]() porta
porta
![]() cariche positive).
cariche positive).
![]() si chiama conducibilita' equivalente e occupa
il posto del termine che avevamo genericamente indicato con
si chiama conducibilita' equivalente e occupa
il posto del termine che avevamo genericamente indicato con
![]() nella relazione precedente (quella in cui usavamo la
concentrazione molare dell'elettrolita).
nella relazione precedente (quella in cui usavamo la
concentrazione molare dell'elettrolita).
48.
Veniamo ora alla seconda complicazione, che riguarda proprio
il termine ![]() . Se
. Se ![]() fosse rigorosamente
proporzionale alla concentrazione equivalente di elettrolita
fosse rigorosamente
proporzionale alla concentrazione equivalente di elettrolita ![]() ,
,
![]() sarebbe indipendente da quest'ultima (per la
definizione stessa di proporzionalita' diretta fra due
grandezze). Cio' che si trova in realta' e' che
sarebbe indipendente da quest'ultima (per la
definizione stessa di proporzionalita' diretta fra due
grandezze). Cio' che si trova in realta' e' che ![]() dipende dalla concentrazione (cioe' da
dipende dalla concentrazione (cioe' da ![]() ): in particolare,
si trova che
): in particolare,
si trova che ![]() diminuisce al crescere della
concentrazione equivalente. Tipici andamenti di
diminuisce al crescere della
concentrazione equivalente. Tipici andamenti di ![]() in
funzione della concentrazione sono mostrati nella
figura 2.3.
in
funzione della concentrazione sono mostrati nella
figura 2.3.
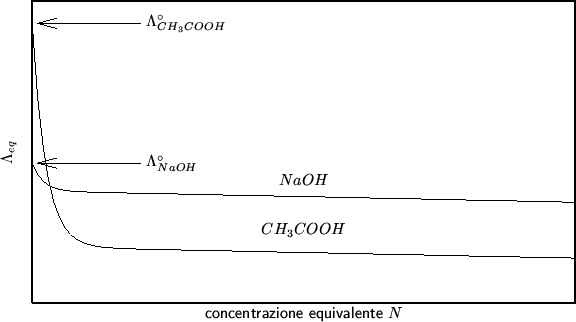 |
Attenti a non fare confusione: stiamo dicendo che ![]() diminuisce al crescere della concentrazione. Per quanto riguarda la
conducibilita' specifica
diminuisce al crescere della concentrazione. Per quanto riguarda la
conducibilita' specifica ![]() , essa generalmente cresce al
crescere della concentrazione, come abbiamo gia' detto in precedenza e
come e' logico aspettarsi alla luce di cio' che abbiamo imparato sul
meccanismo di conduzione dell'elettricita' nelle soluzioni
elettrolitiche (piu' ioni
, essa generalmente cresce al
crescere della concentrazione, come abbiamo gia' detto in precedenza e
come e' logico aspettarsi alla luce di cio' che abbiamo imparato sul
meccanismo di conduzione dell'elettricita' nelle soluzioni
elettrolitiche (piu' ioni ![]() piu' portatori di carica
piu' portatori di carica
![]() piu' corrente). Ricordate che
piu' corrente). Ricordate che ![]() e' legata alla
concentrazione da:
e' legata alla
concentrazione da:
per cui, ad esempio, se ![]() raddoppia,
raddoppia, ![]() diminuisce,
ma la sua diminuzione e' assai minore dell'aumento di
diminuisce,
ma la sua diminuzione e' assai minore dell'aumento di ![]() e quindi,
nel complesso,
e quindi,
nel complesso, ![]() aumenta.
aumenta.
La dipendenza di ![]() dalla concentrazione si puo'
spiegare in modo semplice sulla base di due effetti: il primo e'
costituito dalle interazioni inter-ioniche. Tali interazioni aumentano
all'aumentare della concentrazione perche' gli ioni si incontrano piu'
di frequente e possono associarsi per brevi periodi di tempo: e'
intuitivo che queste associazioni temporanee diminuiscono la
velocita' di migrazione degli ioni e tendono quindi ad ostacolare la
conduzione elettrica.
dalla concentrazione si puo'
spiegare in modo semplice sulla base di due effetti: il primo e'
costituito dalle interazioni inter-ioniche. Tali interazioni aumentano
all'aumentare della concentrazione perche' gli ioni si incontrano piu'
di frequente e possono associarsi per brevi periodi di tempo: e'
intuitivo che queste associazioni temporanee diminuiscono la
velocita' di migrazione degli ioni e tendono quindi ad ostacolare la
conduzione elettrica.
Il secondo effetto riguarda gli elettroliti deboli, cioe' quelle sostanze che si dissociano solo parzialmente. Consideriamo per semplicita' il caso seguente:
Se ![]() e' un elettrolita debole, cio' significa che la costante di
dissociazione
e' un elettrolita debole, cio' significa che la costante di
dissociazione ![]() e' piccola: quindi la concentrazione ionica
effettiva in soluzione e' minore di quello che ci si
potrebbe aspettare sulla base della concentrazione formale
dell'elettrolita; una prima (e ovvia) conseguenza di cio' e' che
generalmente la conducibilita' di un elettrolita debole e' minore di
quella di un elettrolita forte, a parita' di concentrazione. Il grado
di dissociazione
e' piccola: quindi la concentrazione ionica
effettiva in soluzione e' minore di quello che ci si
potrebbe aspettare sulla base della concentrazione formale
dell'elettrolita; una prima (e ovvia) conseguenza di cio' e' che
generalmente la conducibilita' di un elettrolita debole e' minore di
quella di un elettrolita forte, a parita' di concentrazione. Il grado
di dissociazione ![]() e' definito come la frazione di sostanza
inizialmente presente che si dissocia. E' facile (spero) verificare
che per l'equilibrio su scritto, detta
e' definito come la frazione di sostanza
inizialmente presente che si dissocia. E' facile (spero) verificare
che per l'equilibrio su scritto, detta ![]() la concentrazione
iniziale di
la concentrazione
iniziale di ![]() e supponendo che
e supponendo che ![]() sia abbastanza piccola, il
grado di dissociazione e' dato da:
sia abbastanza piccola, il
grado di dissociazione e' dato da:
Questa relazione dice che ![]() diminuisce al crescere
della concentrazione. Siccome il grado di dissociazione e' una misura
diretta di quanti ioni si formano in soluzione a partire da una certa
concentrazione formale di elettrolita, si deduce che la conducibilita'
di una soluzione contenente un elettrolita debole aumenta con la
concentrazione meno di quanto ci si potrebbe aspettare. Tenendo
presente la relazione
diminuisce al crescere
della concentrazione. Siccome il grado di dissociazione e' una misura
diretta di quanti ioni si formano in soluzione a partire da una certa
concentrazione formale di elettrolita, si deduce che la conducibilita'
di una soluzione contenente un elettrolita debole aumenta con la
concentrazione meno di quanto ci si potrebbe aspettare. Tenendo
presente la relazione
![]() , cio' si manifesta in una
diminuzione di
, cio' si manifesta in una
diminuzione di ![]() con la concentrazione. Di nuovo: fate
attenzione; se la concentrazione aumenta, e'
con la concentrazione. Di nuovo: fate
attenzione; se la concentrazione aumenta, e' ![]() che
diminuisce, mentre
che
diminuisce, mentre ![]() aumenta, come ci aspettiamo che debba
essere. Possiamo dire semmai che la diminuzione di
aumenta, come ci aspettiamo che debba
essere. Possiamo dire semmai che la diminuzione di ![]() fa
si' che l'aumento di
fa
si' che l'aumento di ![]() sia inferiore alle previsioni.
sia inferiore alle previsioni.
49.
Per capire meglio consideriamo un caso estremamente
semplificato. Per l'elettrolita debole generico visto sopra,
supponiamo che l'unico effetto non lineare nella relazione fra
![]() ed
ed ![]() sia la non completa dissociazione (questa assunzione
e' molto semplicistica). In altre parole, ammettiamo (ma questo non e'
vero) che
sia la non completa dissociazione (questa assunzione
e' molto semplicistica). In altre parole, ammettiamo (ma questo non e'
vero) che ![]() sia veramente proporzionale alla
concentrazione effettiva di cariche positive (o negative) in
soluzione, cioe':
sia veramente proporzionale alla
concentrazione effettiva di cariche positive (o negative) in
soluzione, cioe':
![]() e' legato alla concentrazione iniziale
e' legato alla concentrazione iniziale ![]() tramite il grado di dissociazione:
tramite il grado di dissociazione:
dove ![]() e' la concentrazione equivalente formale, cioe'
quella che si calcolerebbe in base alla quantita' di sale introdotta
in soluzione. Sostituendo piu' sopra e facendo in modo che compaia un
termine
e' la concentrazione equivalente formale, cioe'
quella che si calcolerebbe in base alla quantita' di sale introdotta
in soluzione. Sostituendo piu' sopra e facendo in modo che compaia un
termine ![]() alla prima potenza si ottiene:
alla prima potenza si ottiene:
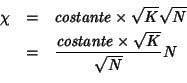
Se confrontiamo questa relazione con la
![]() , ci
rendiamo conto che per questo elettrolita debole la conducibilita'
equivalente e' data da:
, ci
rendiamo conto che per questo elettrolita debole la conducibilita'
equivalente e' data da:
cioe' ![]() dipende dalla concentrazione e diminuisce
all'aumentare di essa. Notate che, comunque,
dipende dalla concentrazione e diminuisce
all'aumentare di essa. Notate che, comunque, ![]() aumenta
con
aumenta
con ![]() . Verificate da soli che:
. Verificate da soli che:
50.
Abbiamo dunque visto che
![]() dipende dalla concentrazione essendo una sua funzione
decrescente. Ovviamente, cio' e' equivalente a dire che
dipende dalla concentrazione essendo una sua funzione
decrescente. Ovviamente, cio' e' equivalente a dire che
![]() aumenta al diminuire della concentrazione ionica in
soluzione: infatti, le interazioni ione-ione si riducono e il grado di
dissociazione aumenta man mano che la concentrazione diminuisce. Per
tutti gli elettroliti si trova sperimentalmente che al diminuire della
concentrazione la conducibilita' equivalente tende ad un valore limite
aumenta al diminuire della concentrazione ionica in
soluzione: infatti, le interazioni ione-ione si riducono e il grado di
dissociazione aumenta man mano che la concentrazione diminuisce. Per
tutti gli elettroliti si trova sperimentalmente che al diminuire della
concentrazione la conducibilita' equivalente tende ad un valore limite
![]() detto conducibilita' equivalente a diluizione
infinita (figura 2.3).
detto conducibilita' equivalente a diluizione
infinita (figura 2.3).
Diversamente da ![]() ,
, ![]() non dipende
dalla concentrazione: infatti, a diluizione infinita (che vuol
dire concentrazione estremamente bassa), le forze ione-ione sono
praticamente assenti perche' gli incontri fra ioni diventano eventi
``rari''. Inoltre anche gli effetti della dissociazione parziale per
gli elettroliti deboli scompaiono perche' a concentrazioni
sufficientemente basse, la dissociazione di un elettrolita debole e'
praticamente completa (trovate la dimostrazione di cio'
nell'appendice B). A quest'ultimo proposito
osservate la figura 2.3: a concentrazioni finite un
elettrolita forte come
non dipende
dalla concentrazione: infatti, a diluizione infinita (che vuol
dire concentrazione estremamente bassa), le forze ione-ione sono
praticamente assenti perche' gli incontri fra ioni diventano eventi
``rari''. Inoltre anche gli effetti della dissociazione parziale per
gli elettroliti deboli scompaiono perche' a concentrazioni
sufficientemente basse, la dissociazione di un elettrolita debole e'
praticamente completa (trovate la dimostrazione di cio'
nell'appendice B). A quest'ultimo proposito
osservate la figura 2.3: a concentrazioni finite un
elettrolita forte come ![]() ha una conducibilita' maggiore di
quella di un elettrolita debole come
ha una conducibilita' maggiore di
quella di un elettrolita debole come ![]() , tuttavia, a
concentrazioni sufficientemente basse, la situazione puo' essere
addirittura invertita.
, tuttavia, a
concentrazioni sufficientemente basse, la situazione puo' essere
addirittura invertita.
51.
Dato che la conducibilita' equivalente a diluizione infinita
![]() dipende solamente dalle caratteristiche del catione
e dell'anione di cui e' composto un elettrolita (e dalle loro
interazioni con il solvente, ma non dalle loro interazioni
reciproche) non stupisce che per essa esista una relazione di
addittivita' nota come legge di Kohlrausch. Per una soluzione
di un solo elettrolita essa assume la forma seguente:
dipende solamente dalle caratteristiche del catione
e dell'anione di cui e' composto un elettrolita (e dalle loro
interazioni con il solvente, ma non dalle loro interazioni
reciproche) non stupisce che per essa esista una relazione di
addittivita' nota come legge di Kohlrausch. Per una soluzione
di un solo elettrolita essa assume la forma seguente:
Nell'espressione appena scritta,
![]() e' la conducibilita'
equivalente a diluizione infinita del catione e
e' la conducibilita'
equivalente a diluizione infinita del catione e
![]() quella
dell'anione dell' elettrolita. Tanto per fare un esempio concreto, la
conducibilita' equivalente per una soluzione di
quella
dell'anione dell' elettrolita. Tanto per fare un esempio concreto, la
conducibilita' equivalente per una soluzione di ![]() infinitamente
diluita e' data da:
infinitamente
diluita e' data da:
La conducibilita' equivalente a diluizione infinita individuale esprime la capacita' di un dato ione di muoversi sotto l'effetto di un campo elettrico in assenza di interazioni con altre specie ioniche.
La cosa importante della legge di Kohlrausch e' che essa permette di
esprimere ![]() come somma di due contributi
indipendenti l'uno dall'altro e caratteristici solamente
del catione e dell'anione di cui e' fatto l'elettrolita. Per soluzioni
contenenti piu' di un elettrolita, la legge si generalizza in:
come somma di due contributi
indipendenti l'uno dall'altro e caratteristici solamente
del catione e dell'anione di cui e' fatto l'elettrolita. Per soluzioni
contenenti piu' di un elettrolita, la legge si generalizza in:
dove la sommatoria e' estesa a tutte le specie ioniche presenti
in soluzione. Ad esempio, per una soluzione infinitamente diluita
contenente ![]() ,
, ![]() e
e ![]() , si ha:
, si ha:
I valori delle conducibilita' equivalenti individuali a diluizione infinita sono sperimentalmente misurabili ed alcuni di essi sono riportati nella tabella 2.1.
|
Possiamo osservare che la maggior parte degli ioni possiede valori di
![]() abbastanza simili: cio' viene generalmente spiegato
col fatto che, a causa dell'idratazione, le dimensioni ioniche sono in
ogni caso simili e questo fa si' che ioni apparentemente molto diversi
abbiano mobilita' simili e quindi capacita' simili di condurre una
corrente elettrica in soluzione. Fanno eccezione gli ioni
abbastanza simili: cio' viene generalmente spiegato
col fatto che, a causa dell'idratazione, le dimensioni ioniche sono in
ogni caso simili e questo fa si' che ioni apparentemente molto diversi
abbiano mobilita' simili e quindi capacita' simili di condurre una
corrente elettrica in soluzione. Fanno eccezione gli ioni ![]() ed
ed
![]() che hanno conducibilita' equivalenti a diluizione infinita
molto maggiori degli altri. Cio' e' dovuto al particolare meccanismo
di migrazione di questi ioni, che si realizza tramite una sorta di
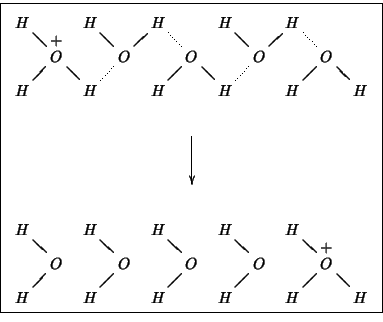
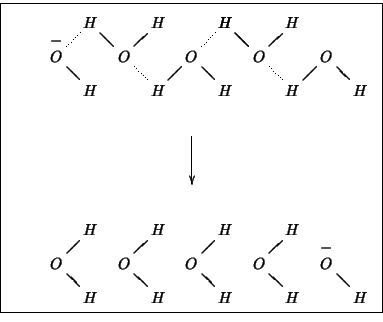
``staffetta'' illustrata nella figura 2.4: in
pratica, grazie alla formazione e rottura di legami idrogeno, si ha
una velocissima migrazione della carica senza che ci sia un
corrispondente movimento effettivo degli ioni.
che hanno conducibilita' equivalenti a diluizione infinita
molto maggiori degli altri. Cio' e' dovuto al particolare meccanismo
di migrazione di questi ioni, che si realizza tramite una sorta di
``staffetta'' illustrata nella figura 2.4: in
pratica, grazie alla formazione e rottura di legami idrogeno, si ha
una velocissima migrazione della carica senza che ci sia un
corrispondente movimento effettivo degli ioni.
|
52.
La legge di Kohlrausch vale
rigorosamente solo a diluizione infinita. Tuttavia, se riguardate la
figura 2.3, osserverete che le variazioni di
![]() a concentrazioni finite non sono molto grandi. In
altre parole, possiamo assumere che una relazione di additivita' sia
approssimativamente valida anche in condizioni ``ordinarie''
(cioe' per concentrazioni non piccolissime). Nei limiti di questa
assunzione possiamo quindi scrivere:
a concentrazioni finite non sono molto grandi. In
altre parole, possiamo assumere che una relazione di additivita' sia
approssimativamente valida anche in condizioni ``ordinarie''
(cioe' per concentrazioni non piccolissime). Nei limiti di questa
assunzione possiamo quindi scrivere:
per un solo elettrolita e:
per il caso di una soluzione contenente piu' elettroliti.
L'assenza degli apici ``![]() '' segnala che le condizioni
non sono di diluizione infinita.
'' segnala che le condizioni
non sono di diluizione infinita.
Deve essere chiaro che, mentre la legge di Kohlrausch (quella con gli
apici ``![]() '') e' rigorosamente valida, quella su scritta e' solo
un'approssimazione. Si trova tuttavia che tale approssimazione e'
ampiamente valida in moltissime applicazioni analitiche della
conduttimetria, come vedremo fra breve.
'') e' rigorosamente valida, quella su scritta e' solo
un'approssimazione. Si trova tuttavia che tale approssimazione e'
ampiamente valida in moltissime applicazioni analitiche della
conduttimetria, come vedremo fra breve.
53. Possiamo finalmente tirare le somme di quanto detto finora e giungere alla relazione fondamentale che lega la conducibilita' misurabile di una soluzione alla concentrazione delle specie ioniche in essa presenti.
Consideriamo prima il caso di un solo elettrolita. Abbiamo visto che la conducibilita' di una sua soluzione e' data da:
Tenete presente che ![]() e' cio' che possiamo misurare
sperimentalmente e
e' cio' che possiamo misurare
sperimentalmente e ![]() si puo' ricavare come detto a
pagina
si puo' ricavare come detto a
pagina ![]() .
.
Abbiamo espresso ![]() come:
come:
dove ![]() e' la concentrazione equivalente dell'elettrolita. Ricordate
che questa concentrazione e' uguale alla concentrazione totale
delle cariche positive o equivalentemente delle cariche negative.
Infine, abbiamo appena visto che, anche se solo approssimativamente,
possiamo esprimere
e' la concentrazione equivalente dell'elettrolita. Ricordate
che questa concentrazione e' uguale alla concentrazione totale
delle cariche positive o equivalentemente delle cariche negative.
Infine, abbiamo appena visto che, anche se solo approssimativamente,
possiamo esprimere ![]() come:
come:
Se combiniamo queste tre relazioni otteniamo:
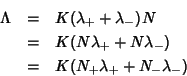
Nell'ultima uguaglianza il termine ![]() sta ad
indicare la concentrazione totale di cariche positive dovute al
catione e il termine
sta ad
indicare la concentrazione totale di cariche positive dovute al
catione e il termine ![]() sta ad indicare la concentrazione totale
di cariche negative dovute all'anione. Per una soluzione contenente un
solo elettrolita, vale chiaramente:
sta ad indicare la concentrazione totale
di cariche negative dovute all'anione. Per una soluzione contenente un
solo elettrolita, vale chiaramente:
Ad esempio, per una soluzione ![]() di
di ![]() si ha
(siatene ben convinti):
si ha
(siatene ben convinti):
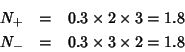
Il motivo per cui abbiamo introdotto le concentrazioni individuali e' che, per il caso generale di una soluzione contenente piu' elettroliti disciolti, la relazione si generalizza in:

Questa espressione e' l'analogo della legge di Nernst vista in potenziometria: essa dice che la conducibilita' di una soluzione elettrolitica e' direttamente proporzionale (entro i limiti dell'approssimazione che abbiamo discusso al punto 52) alle concentrazioni ioniche e costituisce il cardine di tutte le applicazioni analitiche della conduttimetria.
![]() e' la conducibilita' ionica individuale dello ione
i-esimo (positivo o negativo) ed
e' la conducibilita' ionica individuale dello ione
i-esimo (positivo o negativo) ed ![]() e' la concentrazione totale
di cariche di un dato segno ad esso dovute. Ad esempio, per una
soluzione
e' la concentrazione totale
di cariche di un dato segno ad esso dovute. Ad esempio, per una
soluzione ![]() in
in ![]() e
e ![]() in
in
![]() si avrebbe:
si avrebbe:
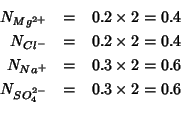
e: