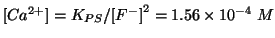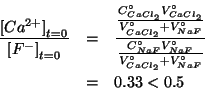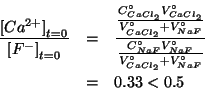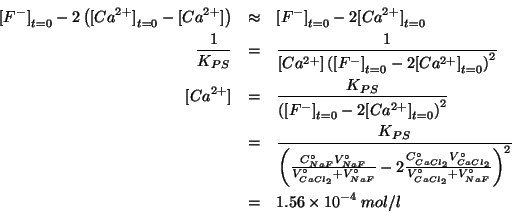


Next: Slide n. 365: solubilita'
Up: Slides delle lezioni del
Previous: Slide n. 363: esempio
Si deve percio' vedere chi e' il reagente limitante:
Il reagente limitante e' lo ione calcio e quindi:
Il calcolo puo' essere eseguito in modo approssimato senza impostare
il trattamento completo dell'equilibrio. Siccome
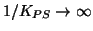 , la reazione si puo' considerare
completa. Inoltre, come gia' visto sopra, siccome
, la reazione si puo' considerare
completa. Inoltre, come gia' visto sopra, siccome
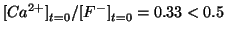 , il
reagente limitante sara'
, il
reagente limitante sara' 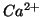 . Quindi, per la concentrazione di
equilibrio dello ione
. Quindi, per la concentrazione di
equilibrio dello ione 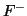 si ha, in prima approssimazione:
si ha, in prima approssimazione:
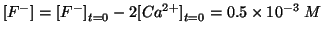 .
A questo punto, la concentrazione di equilibrio degli ioni
.
A questo punto, la concentrazione di equilibrio degli ioni 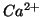 si ricava dalla legge dell'azione di massa utilizzando il valore
approssimato appena trovato per
si ricava dalla legge dell'azione di massa utilizzando il valore
approssimato appena trovato per
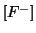 :
: