2000-06-21: mean field analysis

NOTE: the same discussion, with a better notation and extended to cover the activation energy for oxygen migration, is at 2000-08-10 (section 17)

GOAL

Mean field analysis for the $Ce^{4+}/Ce^{3+}$ reduction in $Ce_{(1-x)}Zr_{(x-y)}D_{y}O_{2-\frac{y}{v-1}},\;(v=3,2,\;y<x)$ systems.

Results

Let's take the three cation system $Ce_{(1-x)}Zr_{(x-y)}D_{y}O_{2-\frac{y}{v-1}}$, in which $D$ is a three or two valent dopant (valence$=v=3,2$). Due to the presence of the low valent dopant, the structure will contain a number of compensating oxygen vacancies.

The mean field picture of this fluorite structured mixed oxide is as follows.

The cationic sites are occupied by a hybrid cationic species $M$, built up with a ``linear combination'' of the three cations. In particular, the charge of $M$ is less than $4+$ because of the smaller contribution of $D$; in fact, the charge of $M$ is:

$$\begin{eqnarray*} \overbrace{4(1-x)}^{Ce^{4+}}+\overbrace{4(x-y)}^{Zr^{4+}}+\overbrace{vy}^{D^{v+}}&=&4(1-y)+vy \end{eqnarray*}$$

As far the anionic sites, the mean field approach does not consider them only partially occupied (as they effectively are); instead, they are all occupied by (let's call them) ``mean field'' oxide ions bearing a smaller negative charge. This charge is given by:

$$\begin{eqnarray*} &-2+\frac{y}{v-1}& \end{eqnarray*}$$

i.e. the charge of a ``regular'' oxide ion corrected for the presence of the low valent dopant $D^{v+}$.

If we put a pure $Ce^{4+}$ cation at a cationic site, we create a charged defect; the charge of the defect will be the difference between the charge of a pure $Ce^{4+}$ and that of the hybrid ``mean field'' cation, i.e.:

$$\begin{eqnarray*} 4-\left(4(1-y)+vy\right)&=&y(4-v) \end{eqnarray*}$$

We indicate this defect as: $Ce_{M}^{y(4-v)}$.

In the same way, substitution of a mean field cation $M$ with a pure $Ce^{3+}$ species generates a defect with charge:

$$\begin{eqnarray*} 3-\left(4(1-y)+vy\right)&=&y(4-v)-1 \end{eqnarray*}$$

which we designate as: $Ce_{M}^{y(4-v)-1}$.

A pure oxide ion which sits at an anionic site is seen by the mean field perspective as a defect with charge:

$$\begin{eqnarray*} -2-\left(-2+\frac{y}{v-1}\right)&=&\frac{y}{1-v} \end{eqnarray*}$$

and thus designated as: $O_O^{\frac{y}{1-v}}$.

Finally, a mean field oxide vacancy is to be indicated with $V_O^{2-\frac{y}{v-1}}$.

In the light of the above, the mean field version of the $Ce^{4+}/Ce^{3+}$ reduction reaction can be written as follows:

$$\begin{eqnarray*} 2Ce_{M}^{y(4-v)}+O_O^{\frac{y}{1-v}}&=&2Ce_{M}^{y(4-v)-1}+V_O^{2-\frac{y}{v-1}}+\frac{1}{2}O_{2\;(g)} \end{eqnarray*}$$

This reaction can be decomposed, as usual, into steps whose energy change can be either directly calculated with GULP or is known from the literature:

$$\begin{eqnarray*} 2{Ce^{y(4-v)}_{M}}+2M^{4(1-y)+vy}_{(g)}=2Ce^{4+}_{(g)}+2M^\tim... ..._{M}^{y(4-v)-1}+V_O^{2-\frac{y}{v-1}}+\frac{1}{2}O_{2\;(g)}&&\\ \end{eqnarray*}$$

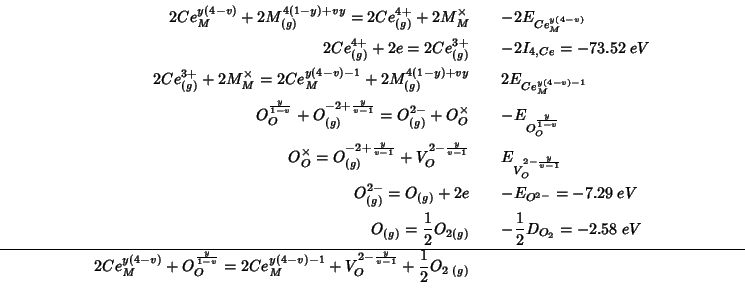
Summing up the various contributions, the $Ce^{4+}/Ce^{3+}$ reduction energy becomes:

$$\begin{eqnarray*} E_{Ce^{4+}/Ce^{3+}}&=&-2E_{Ce^{y(4-v)}_M}-2I_{4,Ce}+2E_{Ce^{y(... ...}_M}-E_{O_O^{\frac{y}{1-v}}}+E_{V_O^{2-\frac{y}{v-1}}}-83.39\;eV \end{eqnarray*}$$

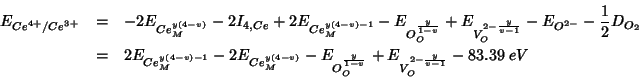
As usual, the constant terms which add up to $-83.39\;eV$ are taken from Table 5 of Sayle et al. (1994). The other energy contributions are evaluated with GULP:

energy term	GULP code
$E_{Ce^{y(4-v)}_M}$	IMPURITY Ce4 0.00 0.00 0.00
$E_{Ce^{y(4-v)-1}_M}$	IMPURITY Ce3 0.00 0.00 0.00
$E_{O_O^{\frac{y}{1-v}}}$	IMPURITY O 0.25 0.25 0.25
$E_{V_O^{2-\frac{y}{v-1}}}$	VACANCY O 0.25 0.25 0.25