Evaluation of the activation energy for oxygen migration in
![]()
Let's re-work the mean field analysis of the
![]() system, including the activation
energy for oxygen migration.
system, including the activation
energy for oxygen migration.
The present discussion is basically equivalent to that at 2000-06-21 (section 2), the only differences being:
![]() is a tri- or di-valent dopant (
is a tri- or di-valent dopant (![]() or
or ![]() ,
respectively). In order to compensate for the lower valence of
,
respectively). In order to compensate for the lower valence of ![]() ,
a number of oxygen vacancies must be distributed in the (supposed)
fluorite structure of the mixed oxide.
,
a number of oxygen vacancies must be distributed in the (supposed)
fluorite structure of the mixed oxide.
If we denote with ![]() the total number of cations in the crystal,
then the ``real'' situation is described as follows:
the total number of cations in the crystal,
then the ``real'' situation is described as follows:
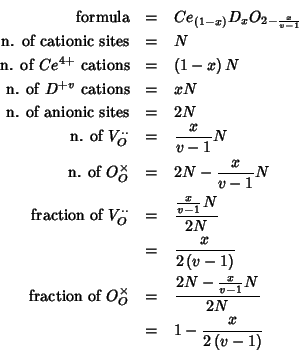
The mean field description of the above system is based on fractional
occupancies: instead of considering the cationic sites as randomly
occupied by distinct ![]() and
and ![]() species, we assume
that each cationic site is occupied by both a
species, we assume
that each cationic site is occupied by both a
![]() and a
and a ![]() cation, in a proportion dictated
by the chemical composition. In a similar way, we do not consider the
anionic sites to be only partially occupied, but we take each anionic
site to be occupied by both an oxide ion and a vacancy, in a
proportion which is again related to the chemical composition.
cation, in a proportion dictated
by the chemical composition. In a similar way, we do not consider the
anionic sites to be only partially occupied, but we take each anionic
site to be occupied by both an oxide ion and a vacancy, in a
proportion which is again related to the chemical composition.
This is equivalent to assume that the crystal is composed by only two
fictitious chemical species: a cation ![]() which results by the
``linear combination'' of a pure
which results by the
``linear combination'' of a pure ![]() and a pure
and a pure ![]() species and an anion
species and an anion ![]() , given by the linear combination of a pure
oxide species and a, let's say,
, given by the linear combination of a pure
oxide species and a, let's say, ![]() species.
species.
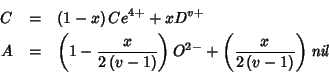
The crystal does not contain different cations and oxygen vacancies
any more; rather, all crystal sites of a given type (cationic or
anionic) are identical and contain the same (hybrid) species. It
follows that the ``mean field'' formula of the mixed oxide is to be
written as ![]() , with
, with ![]() and
and ![]() defined above.
defined above.
The properties of the ``mean field species'' are averages derived from
those of pure component species. In particular, the electric charges
![]() and
and ![]() are given by:
are given by:
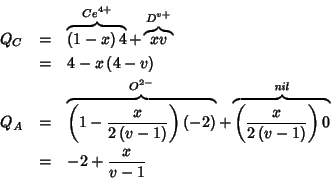
The charge of a substitutional point defect is given by the difference
between the charge of the substitutional and the charge of the crystal
species being substituted. It follows that in the mean field
treatment, putting, say, a pure ![]() species at a cationic site
of the lattice will give raise to a charged defect, whose charge is:
species at a cationic site
of the lattice will give raise to a charged defect, whose charge is:
![]() . The most
interesting (for us) point defects are reported below:
. The most
interesting (for us) point defects are reported below:
![$V_A^{\left[0-\left(-2+\frac{x}{v-1}\right)\right]}=V_A^{2-\frac{x}{v-1}}$](img226.gif)
![$O_A^{\left[-2-\left(-2+\frac{x}{v-1}\right)\right]}=O_A^{-\frac{x}{v-1}}$](img229.gif)
We now turn our attention to the
![]() reduction in a
reduction in a
![]() mixed oxide.
mixed oxide.
The usual formulation of the reaction would be:
whose meaning is: two ![]() cations at their lattice sites
become two reduced
cations at their lattice sites
become two reduced ![]() species at the same sites; at the same
time, one oxide ion is released as gaseous oxygen, leaving a
corresponding vacancy at an anionic site.
species at the same sites; at the same
time, one oxide ion is released as gaseous oxygen, leaving a
corresponding vacancy at an anionic site.
The equivalent formulation in the mean field frame is a bit different, for we have to reformulate the pure species as charged defects, as discussed above:
This reaction can be decomposed, as usual, into steps whose energy change can be either directly calculated with GULP or is known from the literature:
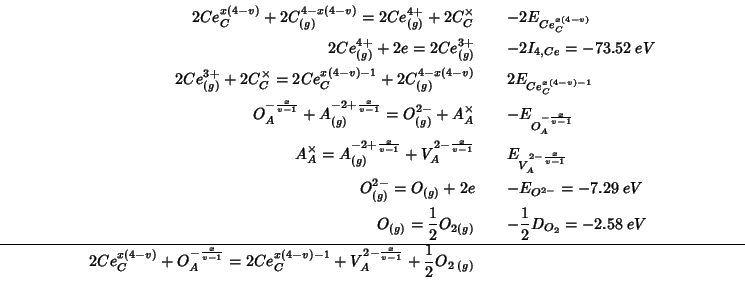
Summing up the various contributions, the
![]() reduction energy becomes:
reduction energy becomes:
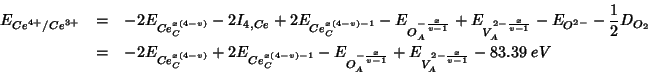
As usual, the constant terms which add up to ![]() are taken
from Table 5 of Sayle et al. (1994). The other energy contributions are
evaluated with GULP:
are taken
from Table 5 of Sayle et al. (1994). The other energy contributions are
evaluated with GULP:
| energy term | GULP code |
|
|
IMPURITY Ce4 0.00 0.00 0.00 |
|
|
IMPURITY Ce3 0.00 0.00 0.00 |
|
|
IMPURITY O 0.25 0.25 0.25 |
|
|
VACANCY O 0.25 0.25 0.25 |
We now consider the migration of oxide ions. The activation energy for oxygen migration is evaluated as the difference between the energy of the ``activated state'' and the energy of the corresponding reference state. The reference state is an oxide ion at an anionic site of the lattice having an available vacant anionic site in nearest neighbor position. The ``activated state'' is taken to consist of the migrating oxide ion along the migration path towards the vacant site, in a position which maximizes the energy of the system. The process can be depicted as follows:
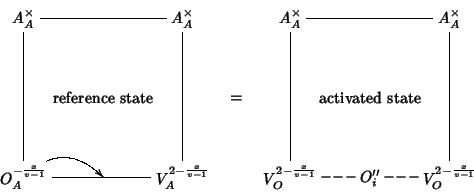
Using our mean field notation, the process can be described by the following equation:
The defect cluster on the LHS indicates a pure oxide ion at an anionic site with a neighboring vacancy (see picture above); the defect cluster on the RHS stands for a pure oxide ion at an interstitial site (the exact position is the one which maximizes the energy) with two neighboring vacancies.
As said before, an estimate of the activation energy for oxygen migration is given by the energy change for this reaction.
The decomposition of the reaction into steps whose energy change can be calculated directly with GULP is as follows:
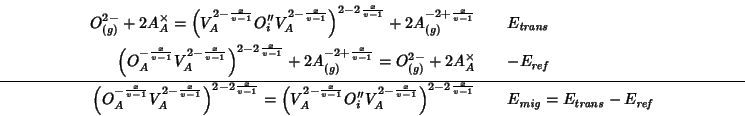
The two component energies are evaluated with GULP using the following directives:
IMPURITY O 0.25 0.25 0.25 VACANCY 0.75 0.25 0.25
bulk_nooptimize trans defect ... VACANCY 0.25 0.25 0.25 VACANCY 0.75 0.25 0.25 INTERSTITIAL O 0.45 0.23 0.27 ...
For all compositions the position of the migrating oxide in the ``activated state'' found by GULP was exactly midway between the two vacant sites.
Taking the cluster described in the previous mean field analysis as reference state one gets negative activation energies:
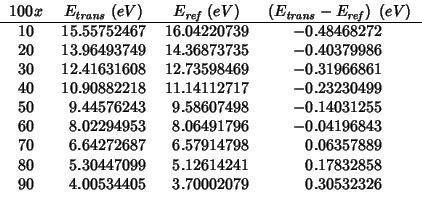
This is because the energy profile for an interstitial oxide moving
along the line between two nearest-neighbor anionic sites has a
maximum midway (as expected and found by the `` trans''
calculations), but also two symmetrical minima near the anionic
sites. The following is a plot of the energy profile for the
![]() composition (obtained with `` INTERSTITIAL O
composition (obtained with `` INTERSTITIAL O
![]() FIX''):
FIX''):
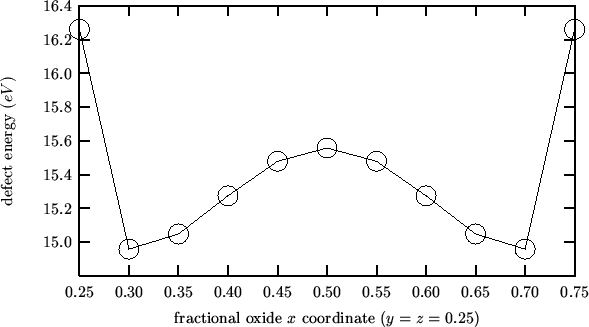
In the light of these findings, the activation energy for oxygen migration should be evaluated according to the following procedure:
For the reasons explained in the ceria-![]() subsection, I have
not evaluated the
subsection, I have
not evaluated the
![]() term.
term.
For the reasons explained in the ceria-![]() subsection, I have
not evaluated the
subsection, I have
not evaluated the
![]() term.
term.
For the reasons explained in the ceria-![]() subsection, I have
not evaluated the
subsection, I have
not evaluated the
![]() term.
term.

The trans run has to be done with an already optimized bulk structure. Hence there are two steps:
opti conp
dump every 1 la-bulk-60.dump
maxcyc opt 200
maxcyc fit 200
title
Activation energy for oxygen migration in Ce_{1-x}La_xO_{2-\frac{x}{2}}
end
cell
5.329267 5.329267 5.329267 90.000000 90.000000 90.000000
fractional 5
Ce4 core 0.0000 0.0000 0.0000 -3.7000 0.4000 0.0000
La core 0.0000 0.0000 0.0000 3.0000 0.6000 0.0000
O core 0.2500 0.2500 0.2500 0.0770 0.8500 0.0000
Ce4 shel 0.0000 0.0000 0.0000 7.7000 0.4000 0.0000
O shel 0.2500 0.2500 0.2500 -2.0770 0.8500 0.0000
space
225
size 10.45067684 21.94642136
centre 0.50 0.25 0.25
interstitial O 0.45 0.23 0.27
vacancy 0.25 0.25 0.25
vacancy 0.75 0.25 0.25
buck
Ce4 shel O shel 1986.8300 0.351070 20.400 0.000 15.000
La core O shel 1439.7 0.36510 0.0 0.0 15.0
O shel O shel 22764.300 0.149000 27.890 0.000 15.000
spring
Ce4 291.75000
O 27.290000
#
# Keywords:
#
bulk_nooptimize trans defect
#
# Options:
#
title
Activation energy for oxygen migration in Ce_{1-x}La_xO_{2-\frac{x}{2}}
end
cell
5.586480 5.586480 5.586480 90.000000 90.000000 90.000000
fractional 5
Ce4 core 0.0000000 0.0000000 0.0000000 -3.7000000 0.40000 0.00000
La core 0.0000000 0.0000000 0.0000000 3.00000000 0.60000 0.00000
O core 0.2500000 0.2500000 0.2500000 0.07700000 0.85000 0.00000
Ce4 shel 0.0000000 0.0000000 0.0000000 7.70000000 0.40000 0.00000
O shel 0.2500000 0.2500000 0.2500000 -2.0769999 0.85000 0.00000
space
225
centre 0.5000 0.2500 0.2500
size 10.4507 21.9464
vacancy 0.250000 0.250000 0.250000
vacancy 0.750000 0.250000 0.250000
interstitial O 0.450000 0.230000 0.270000
buck
O shel Ce4 shel 1986.8300 0.351070 20.400 0.000 15.000
buck
La core O shel 1439.7000 0.365100 .00000E+00 0.000 15.000
buck
O shel O shel 22764.300 0.149000 27.890 0.000 15.000
spring
Ce4 291.75000
spring
O 27.290000
maxcyc opt 200
maxcyc fit 200
dump every 1 la-trans-60.dump
NOTE: the input for the trans calc can be generated automatically from the dump file of the bulk optimization in a shell script. E.g.:
... gulp < la-bulk-60 > la-bulk-60.out wait sed -e's/^opti conp *$/bulk_nooptimize trans defect/' \ -e'/^dump every/s/la-bulk/la-trans/' la-bulk-60.dump > la-trans-60 gulp < la-trans-60 > la-trans-60.out wait ...