next up previous contents
Next: 2000-08-04: ``Strict'' reproduction of Up: Aliovalent cation doped ceria Previous: 2000-07-31: updated summary for


2000-07-31a: comparison with experimental data

GOAL

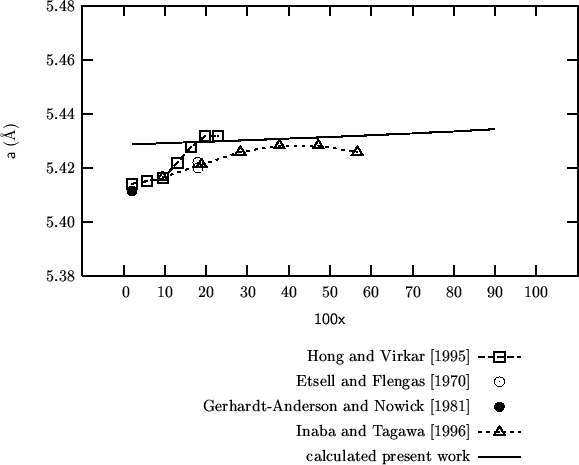
Comparison of calculated vs experimental lattice parameters for $Ce_{(1-x)}D_xO_{2-\frac{x}{2}}, D=Y,Gd,La$ at different compositions.

Results

$Ce_{(1-x)}La_xO_{2-\frac{x}{2}}$

Hong and Virkar (1995)

Some experimental lattice parameters for $Ce_{(1-x)}La_xO_{2-\frac{x}{2}}$ with $0.02\leq{}x\leq0.23$ can be derived from fig. 4 of this paper.

\begin{threeparttable} \begin{tabular}{D{.}{.}{-1}D{.}{.}{-1}D{.}{.}{-1}D{.}{.}{... ...48-5.36}{61}\frac{\mbox{{\it {}\AA}}}{mm}$} \end{tablenotes}\end{threeparttable}

Etsell and Flengas (1970)

A value of $5.451\;\mbox{{\it {}\AA}}$ for the lattice parameter of the $CeO_2+10\%La_2O_3$ system is quoted on p. 366. The formulation of a binary system expressed as $CeO_2+P\%D_2O_3$ with our present notation $Ce_{(1-x)}D_xO_{\left(2-\frac{x}{2}\right)}$ is as follows:


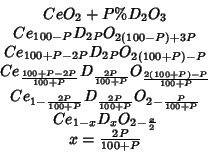
\begin{displaymath} \begin{array}{c} CeO_2+P\%D_2O_3\\ Ce_{100-P}D_{2P}O_{2\lef... ..._{1-x}D_xO_{2-\frac{x}{2}}\\ x=\frac{2P}{100+P}\\ \end{array}\end{displaymath}

So the value quoted by Etsell and Flengas refers to the system of composition:

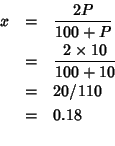
\begin{eqnarray*} x&=&\frac{2P}{100+P}\\ &=&\frac{2\times10}{100+10}\\ &=&20/110\\ &=&0.18\\ \end{eqnarray*}



Gerhardt-Anderson (1981)

In table 1 of this paper the per cent lattice parameter change per unit dopant concentration is reported for systems of the type: $CeO_2+P\%M_2O_3\;M=La,Gd,Y,Sc$.

I disagree with the way data are presented because reporting the quantity $\frac{1}{C_\circ}\frac{\Delta{}a}{a}$ without quoting the composition at which it was determined implicitly assumes a linear relation between the lattice parameter and the composition, which is not at all guaranteed. Taking the ceria-lanthana system as an example, one could say:

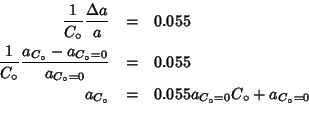
\begin{eqnarray*} \frac{1}{C_\circ}\frac{\Delta{}a}{a}&=&0.055\\ \frac{1}{C_\ci... ....055\\ a_{C_\circ}&=&0.055a_{C_\circ=0}C_\circ+a_{C_\circ=0}\\ \end{eqnarray*}



which would give the lattice parameter at any dopant concentration once the value for pure ceria is assigned (e.g. $a_{C_\circ=0}=5.411\;\mbox{{\it {}\AA}}$).

Actually, this seems to have been done in figs. 7-10 of Minervini et al. (1999) for a (not so) small composition range ( $0.0\leq{}x\leq0.25$ for the system $Ce_{1-2x}M_{2x}O_{2-x}$).

However, since it appears that the data in table 1 were collected for systems of the type $CeO_2+1\%M_2O_3$ (see the second paragraph of the second column on p. 548), I think that it's more correct to take the lattice parameters as referring to this single composition, which corresponds to $x=2/101=0.02$ for the system formulated as $Ce_{1-x}M_xO_{2-\frac{x}{2}}$.

Given the above, the experimental value which can be extracted from this paper for the lattice parameter of the $Ce_{1-x}La_xO_{2-\frac{x}{2}}$ system is:

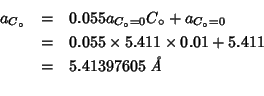
\begin{eqnarray*} a_{C_\circ}&=&0.055a_{C_\circ=0}C_\circ+a_{C_\circ=0}\\ &=&0.... ...mes5.411\times0.01+5.411\\ &=&5.41397605\;\mbox{{\it {}\AA}}\\ \end{eqnarray*}



for $x=0.02$.

Inaba and Tagawa (1996)

Fig. 8 of this paper reproduces the lattice parameter variation as a function of composition for a series of doped cerias from the work of Bevan and Summerville (1979). (The same work is cited by Minervini et al. (1999), but the citation seems to be different and also the data shown in fig. 7 of Grimes' paper do not look the same as those in fig. 8 of Inaba's paper: ?????)

\begin{threeparttable} \begin{tabular}{D{.}{.}{-1}D{.}{.}{-1}D{.}{.}{-1}D{.}{.}{... ...5.6-5.2}{85}\frac{\mbox{{\it {}\AA}}}{mm}$} \end{tablenotes}\end{threeparttable}

Bernal et al. (1997)

Table 1 of this paper reports the lattice parameter for three compositions:

\fpDecimalSign{.}\rcRoundingfalse \begin{tabular}{R{1}{2}R{1}{3}} \multicolumn{1... ...}\AA}})$}} \\ \hline 0.2 & 5.48 \\ 0.4 & 5.54 \\ 0.57 & 5.61 \\ \end{tabular}

Some additional calculated data on lattice parameter

For better comparison I've evaluated some additional data in the interval $0.02\leq{}x\leq0.24$.

\begin{tabular}{D{.}{.}{-1}D{.}{.}{-1}} \multicolumn{1}{c}{{$x$}} &\multicolumn{... ...86 \\ 0.20 & 5.477207 \\ 0.22 & 5.482274 \\ 0.24 & 5.487374 \\ \end{tabular}

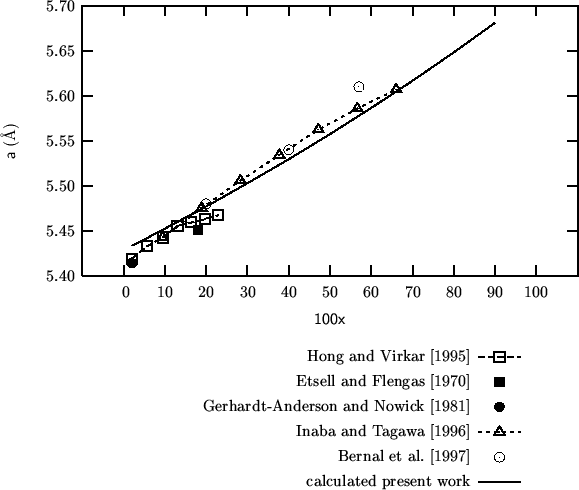
\begin{center}\vbox{\input{2000-07-31a-01.pslatex} }\end{center}

$Ce_{(1-x)}Y_xO_{2-\frac{x}{2}}$

Etsell and Flengas (1970)

The following values are reported on p. 366 for the lattice parameter of the $CeO_2+10\%Y_2O_3$ system (equivalent to $Ce_{(1-0.18)}Y_{0.18}O_{\left(2-\frac{0.18}{2}\right)}$): $5.408,5.405,5.404\;\mbox{{\it {}\AA}}$.

Gerhardt-Anderson (1981)

From table 1 of this paper the following value of the lattice parameter for the system $Ce_{(1-0.02)}Y_{0.02}O_{\left(2-\frac{0.02}{2}\right)}$ can be obtained (notation and comments on this paper to be found above):

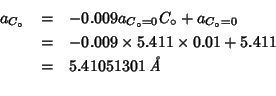
\begin{eqnarray*} a_{C_\circ}&=&-0.009a_{C_\circ=0}C_\circ+a_{C_\circ=0}\\ &=&-... ...mes5.411\times0.01+5.411\\ &=&5.41051301\;\mbox{{\it {}\AA}}\\ \end{eqnarray*}



Inaba and Tagawa (1996)

From fig. 8 of this paper (comments to be found above):

\begin{threeparttable} \begin{tabular}{D{.}{.}{-1}D{.}{.}{-1}D{.}{.}{-1}D{.}{.}{... ...5.6-5.2}{85}\frac{\mbox{{\it {}\AA}}}{mm}$} \end{tablenotes}\end{threeparttable}

Hartridge et al. (1998)

From fig. 4 of this paper:

\begin{threeparttable} \begin{tabular}{D{.}{.}{-1}D{.}{.}{-1}D{.}{.}{-1}} \multi... ...0-5.375}{17}\frac{\mbox{{\it {}\AA}}}{mm}$} \end{tablenotes}\end{threeparttable}

Some additional calculated data on lattice parameter

For better comparison I've evaluated some additional data in the interval $0.02\leq{}x\leq0.24$.

\begin{tabular}{D{.}{.}{-1}D{.}{.}{-1}} \multicolumn{1}{c}{{$x$}} &\multicolumn{... ...65 \\ 0.20 & 5.413241 \\ 0.22 & 5.411598 \\ 0.24 & 5.409897 \\ \end{tabular}

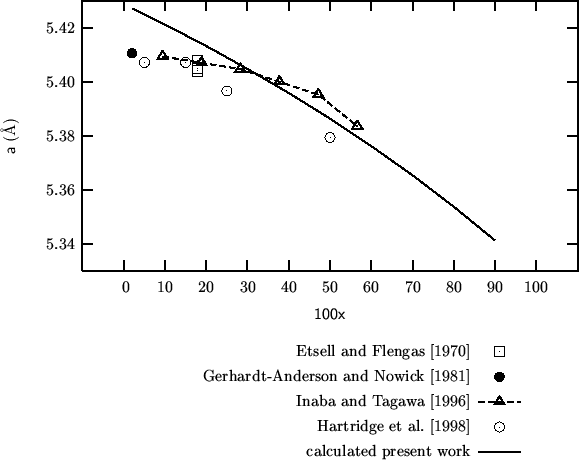
\begin{center}\vbox{\input{2000-07-31a-02.pslatex} }\end{center}

$Ce_{(1-x)}Gd_xO_{2-\frac{x}{2}}$

Hong and Virkar (1995)

Some experimental lattice parameters for $Ce_{(1-x)}Gd_xO_{2-\frac{x}{2}}$ with $0.02\leq{}x\leq0.23$ can be derived from fig. 4.

\begin{threeparttable} \begin{tabular}{D{.}{.}{-1}D{.}{.}{-1}D{.}{.}{-1}D{.}{.}{... ...48-5.36}{61}\frac{\mbox{{\it {}\AA}}}{mm}$} \end{tablenotes}\end{threeparttable}

Etsell and Flengas (1970)

The following values are reported on p. 366 for the lattice parameter of the $CeO_2+10\%Gd_2O_3$ system (equivalent to $Ce_{(1-0.18)}Gd_{0.18}O_{\left(2-\frac{0.18}{2}\right)}$): $5.420,5.422\;\mbox{{\it {}\AA}}$.

Gerhardt-Anderson (1981)

From table 1 of this paper the following value of the lattice parameter for the system $Ce_{(1-0.02)}Gd_{0.02}O_{\left(2-\frac{0.02}{2}\right)}$ can be obtained (notation and comments on this paper to be found above):

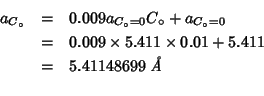
\begin{eqnarray*} a_{C_\circ}&=&0.009a_{C_\circ=0}C_\circ+a_{C_\circ=0}\\ &=&0.... ...mes5.411\times0.01+5.411\\ &=&5.41148699\;\mbox{{\it {}\AA}}\\ \end{eqnarray*}



Inaba and Tagawa (1996)

From fig. 8 of this paper (comments to be found above):

\begin{threeparttable} \begin{tabular}{D{.}{.}{-1}D{.}{.}{-1}D{.}{.}{-1}D{.}{.}{... ...5.6-5.2}{85}\frac{\mbox{{\it {}\AA}}}{mm}$} \end{tablenotes}\end{threeparttable}

Some additional calculated data on lattice parameter

For better comparison I've evaluated some additional data in the interval $0.02\leq{}x\leq0.24$.

\begin{tabular}{D{.}{.}{-1}D{.}{.}{-1}} \multicolumn{1}{c}{{$x$}} &\multicolumn{... ...75 \\ 0.20 & 5.429681 \\ 0.22 & 5.429788 \\ 0.24 & 5.429897 \\ \end{tabular}

\begin{center}\vbox{\input{2000-07-31a-03.pslatex} }\end{center}

next up previous contents
Next: 2000-08-04: ``Strict'' reproduction of Up: Aliovalent cation doped ceria Previous: 2000-07-31: updated summary for