In the
![]() system, oxygen sites are only
partially occupied. This means that GULP assigns a scaled
charge to the oxygen ions: in other words, each anion site is assumed
to contain a
system, oxygen sites are only
partially occupied. This means that GULP assigns a scaled
charge to the oxygen ions: in other words, each anion site is assumed
to contain a ![]() ion, instead of the
ion, instead of the ![]() oxide
species. To put it another way, the following correspondence is
established:
oxide
species. To put it another way, the following correspondence is
established:
| REAL SYSTEM | MEAN FIELD ( GULP) | ||
|
|
From the mean field viewpoint, the water incorporation reaction should be written in the following way:
where ![]() is an oxygen site vacancy, whose charge is
is an oxygen site vacancy, whose charge is
![]() and not
and not ![]() , since GULP treats each oxygen as
having a charge of
, since GULP treats each oxygen as
having a charge of ![]() because of partial occupancy;
because of partial occupancy;
![]() means ``a real
means ``a real ![]() ion (because we
need that to make up an
ion (because we
need that to make up an ![]() group) at an anionic site'': since the
anionic site has charge
group) at an anionic site'': since the
anionic site has charge ![]() , an
, an ![]() oxide at that site
will have a charge of
oxide at that site
will have a charge of ![]() ; finally, the actual charge on the
; finally, the actual charge on the
![]() defect will be
defect will be ![]() and not
and not ![]() for the same
reasons.
for the same
reasons.
What we actually can evaluate with GULP is the energy change for the following processes:
The evaluation of the above energy terms is coded in GULP as
follows ( O1 is a ``genuine'' ![]() , while O2 and
H2 are the oxyegn and hydrogen atoms of the
, while O2 and
H2 are the oxyegn and hydrogen atoms of the ![]() group):
group):
| energy | eqn. | GULP code |
|
|
(2) | IMPURITY O1 0.25 0.25 0.25 |
|
|
(3) | VACANCY 0.25 0.25 0.25 |
|
|
(4) | IMPURITY O2 CORE 0.25 0.25 0.25 |
| INTERSTITIAL H2 CORE 0.3735 0.3735 0.25 |
Equation 1 can be decomposed in terms of equations 2-4 and of the usual gas phase reaction 5
We have:
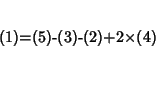
or:
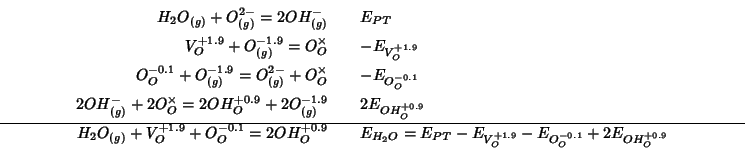
![]() and
and ![]() are not directly evaluated with
GULP: the energies that we can calculate directly with
GULP are only those for
processes 2-4.
are not directly evaluated with
GULP: the energies that we can calculate directly with
GULP are only those for
processes 2-4.
However, steps 6 and 7 can be expressed as proper combinations of processes 2-4.
For step 6 we have:
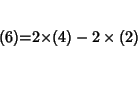
or:
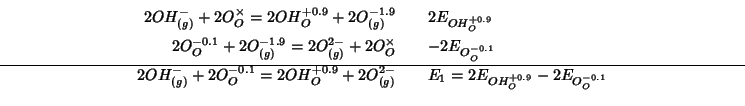
For step 7 we have:
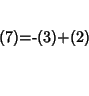
or:
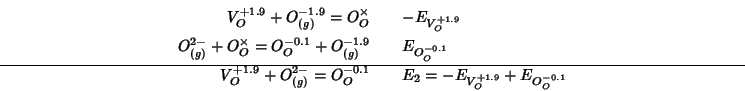
Using the values so obtained for ![]() and
and ![]() , the final
expression for
, the final
expression for ![]() is obtained:
is obtained:
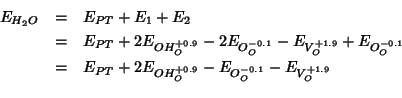
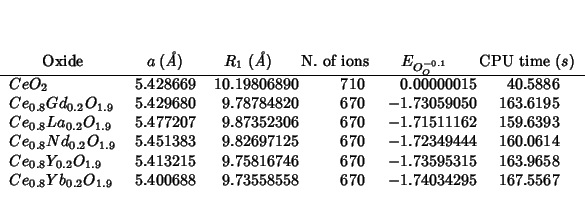
Taking the
![]() values from 2000-02-23 and the
values from 2000-02-23 and the
![]() values from 2000-02-02, we have:
values from 2000-02-02, we have:

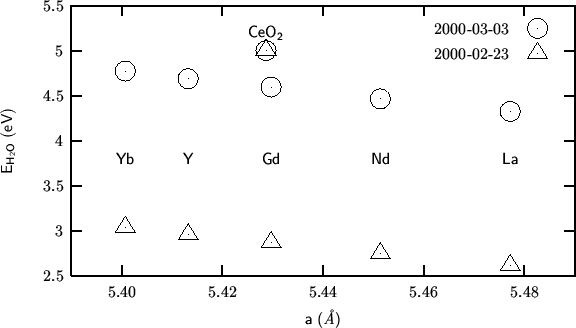
As expected, the mean field correction is zero for pure
ceria. For the doped systems, its effect is that of increasing the
![]() values, making the difference with pure ceria much
smaller. This sounds reasonable. Water incorporation is still more
unfavorable for pure than the doped cerias. The problem is that the
trend within the mixed systems is still opposite with the experimental
one.
values, making the difference with pure ceria much
smaller. This sounds reasonable. Water incorporation is still more
unfavorable for pure than the doped cerias. The problem is that the
trend within the mixed systems is still opposite with the experimental
one.
opti conp defect regi_before #conp defect single dump every 1 nd-O-impurity.dump maxcyc 200 cutb 3.0 # what does this mean? Ronny uses it. title Neodymium solid solution N.Sakai et al. Solid State Ionics 125(1999)325-331 end cell 5.490000 5.490000 5.490000 90.000000 90.000000 90.000000 size 9.82697125 20.0 centre 0.25 0.25 0.25 #vacancy 0.25 0.25 0.25 impurity O1 0.25 0.25 0.25 fractional ############ # Cores ############ Ce4 core 0.000000 0.000000 0.000000 -3.700000 0.8 Nd core 0.000000 0.000000 0.000000 3.00 0.2 O1 core 0.250000 0.250000 0.250000 0.07700 0.95 ############ # Shells ############ Ce4 shel 0.000000 0.000000 0.000000 7.700000 0.8 O1 shel 0.250000 0.250000 0.250000 -2.07700 0.95 space 225 ######################### # Shell-core charges ######################### species Ce3 shel 7.700000 Ce3 core -4.700000 O2 core -1.4263 H2 core 0.4263 ######################### # Short range potentials ######################### buck Ce4 shel O1 shel 1986.830000 0.351070 20.40000 0.0 15.000 Ce3 shel O1 shel 1731.61808 0.36372 14.43256 0.0 15.000 Nd core O1 shel 1379.9 0.36010 0.00000 0.0 15.000 O1 shel O1 shel 22764.300000 0.149000 27.89000 0.0 15.000 O2 core O1 shel 22764.300000 0.149000 27.89000 0.0 15.000 H2 core O1 shel 311.970 0.35 0.0 0.0 15.000 Ce4 shel O2 core 1986.830000 0.351070 20.40000 0.0 15.000 Nd core O2 shel 1379.9 0.36010 0.00000 0.0 15.000 morse H2 core O2 core 7.05250 2.19860 0.9485 1.0 0.0 2.0 ######################### # Spring parameters ######################### spring Ce4 291.750000 Ce3 291.750000 O1 27.29