Gabriele Balducci
last update: August 18, 1999
NOTE: the ``INVERSE'' part of the Buckingham potential is taken ``as is'': this means that the minus sign must be included in the input (see below and the ``SHELL user's guide'')
TITLE ceria structure optimization
LATTICE CP 5.429078
PARTICLES
Ce-shel 0.0 7.7
Ce-core 140.12 -3.7
O-shel 0.0 -2.077
O-core 16.0 0.077
BASIS
Ce-core 0.0 0.0 0.0
Ce-core 0.5 0.5 0.0
Ce-core 0.5 0.0 0.5
Ce-core 0.0 0.5 0.5
O-core 0.25 0.25 0.25
O-core 0.75 0.25 0.25
O-core 0.75 0.75 0.25
O-core 0.25 0.75 0.25
O-core 0.25 0.25 0.75
O-core 0.75 0.25 0.75
O-core 0.75 0.75 0.75
O-core 0.25 0.75 0.75
#
Ce-shel 0.0 0.0 0.0
Ce-shel 0.5 0.5 0.0
Ce-shel 0.5 0.0 0.5
Ce-shel 0.0 0.5 0.5
O-shel 0.25 0.25 0.25
O-shel 0.75 0.25 0.25
O-shel 0.75 0.75 0.25
O-shel 0.25 0.75 0.25
O-shel 0.25 0.25 0.75
O-shel 0.75 0.25 0.75
O-shel 0.75 0.75 0.75
O-shel 0.25 0.75 0.75
POTENTIALS
EXPO Ce-shel O-shel 1986.83 0.351070 0.0 10.0
INVERSE Ce-shel O-shel -20.4 6.0 0.0 10.0
EXPO O-shel O-shel 22764.300 0.149000 0.0 10.0
INVERSE O-shel O-shel -27.89 6.0 0.0 10.0
SPRING Ce-shel Ce-core 291.75 0.0 0.2
SPRING O-shel O-core 27.29 0.0 0.2
CUTSHELL 0.3
OPTION
MESH 0
TEMP 0.0
PRESS 0.0
RUN THERMO
END
CONTROL:
pure ceria, to check the SHELL code
zero
pres 0.001013 kbar (0.001013 kbar=1.0 atm)
steps 1
equilibration steps 0
timestep 0.002 ps
multiple timestep 1
scale 1
cutoff 8.00 # maximum allowed value from genlat
delr 1.0
rdf sampling every 1 steps
print rdf
eps 1.0
ewald precision 1.0e-5
ensemble nve
stats 1
trajectory nstraj 1 istraj 1 keytrj 0
stack 1
job time 10700
close time 300
finish
FIELD:
CeO_2
units eV
molecular types 2
CeriumFour
nummols 108
atoms 1
Ce4 140.120 4.0
finish
Oxygen
nummols 216
atoms 2
O 14.40000 0.077 1
O_s 1.600000 -2.077 1
shell 1
1 2 27.29
finish
vdw 2
Ce4 O_s buck 1986.830000 0.351070 20.40000
O_s O_s buck 22764.300 0.149000 27.89000
CLOSE
A good accord is found.
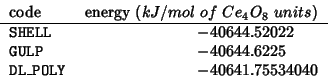
Five runs with increasing MESH values were performed, each
consisting of an OPTIMISE CELL optimization at ![]() and
and
![]()
Gibbs free energy and lattice constant seem to converge properly.
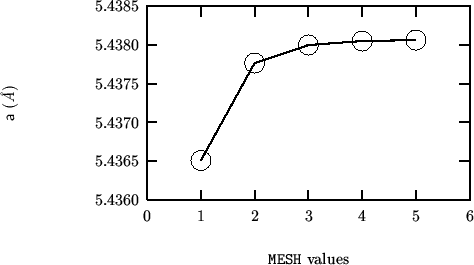
We simulate the ceria-zirconia solid solution by creating an hybrid cation with properties scaled according to the composition.
If we call:
| the hybrid cation | |
| zzirconia fraction in the solid solution | |
| molar mass of species |
|
| shell charge of species |
|
| Buckingham potential for the interaction of |
|
| spring potential between core and shell of |
then we have:
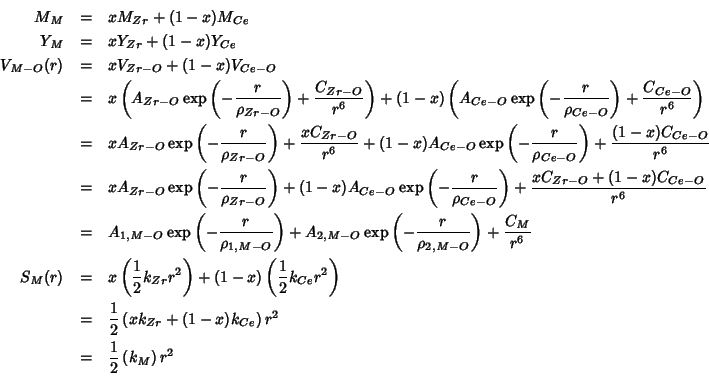
( We write ![]() , so that
, so that ![]() 's are negative, as
SHELL requires that)
's are negative, as
SHELL requires that)
The values to be combined are:

These are the values of the hybrid properties as a function of the zirconia fraction:
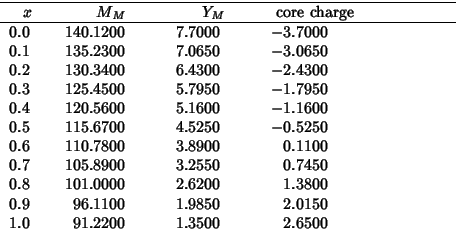
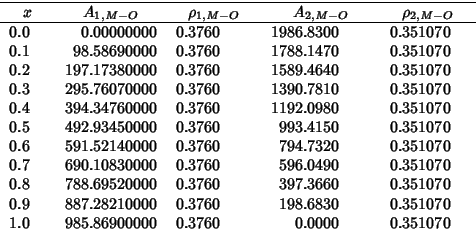
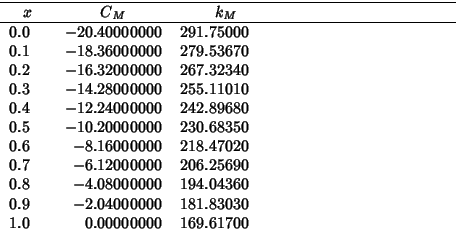
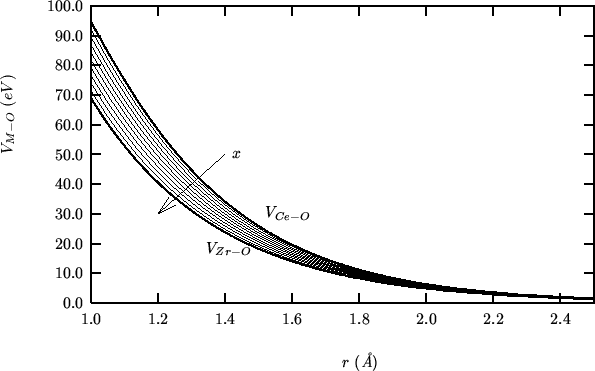
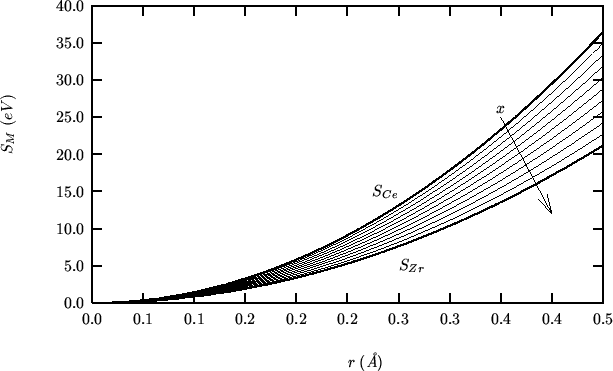
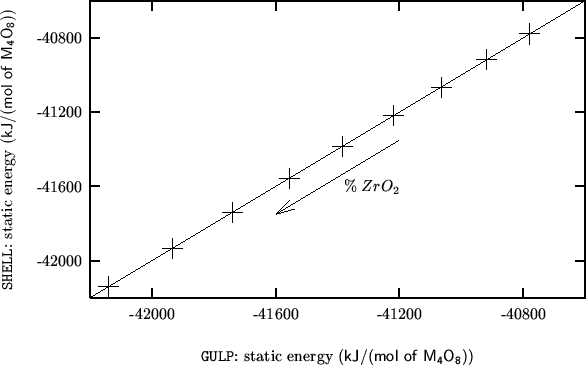
The following compares SHELL vs GULP for a static single point energy calculation on the complete range of compositions:
| GULP | SHELL | ||
| 10 | -40778.0111 | -40777.89813 |
|
| 20 | -40917.8574 | -40917.74343 |
|
| 30 | -41065.2598 | -41065.14482 |
|
| 40 | -41219.8563 | -41219.74031 |
|
| 50 | -41382.9012 | -41382.78406 |
|
| 60 | -41555.2593 | -41555.14099 |
|
| 70 | -41738.1029 | -41737.98320 |
|
| 80 | -41932.2041 | -41932.08300 |
|
| 90 | -42139.1513 | -42139.02862 |
|
Same as above, but in a graphical form:
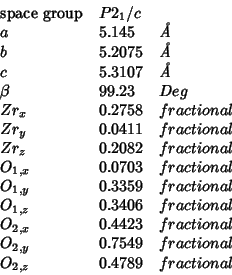
Structural determinations of monoclinic zirconia (baddeleyte) can be found in references smith:65, mccullough:59 and adam:59.
The following are the structural parameters from ref. smith:65:
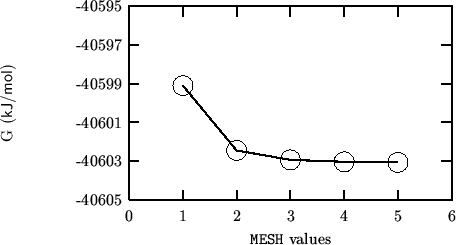
The following compares SHELL and GULP results for a static cell only optimisation:

The following compares SHELL and GULP results for a static, symmetry constrained (cell+coordinates) optimisation: