


Next: Slide n. 103: l'andamento
Up: Slides delle lezioni del
Previous: Slide n. 101: la
- Un'utile rappresentazione e' quella di riportare in un grafico
bidimensionale la cosiddetta densita' di probabilita'
radiale. Questa non e' altro che la probabilita' di trovare
l'elettrone in un guscio sferico di raggio
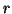 e spessore
infinitesimo
e spessore
infinitesimo 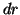 centrato sul nucleo e si deriva dal quadrato del
modulo dell'orbitale. Dall'analisi degli andamenti che si ottengono
per i vari orbitali
centrato sul nucleo e si deriva dal quadrato del
modulo dell'orbitale. Dall'analisi degli andamenti che si ottengono
per i vari orbitali 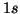 ,
, 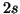 , etc si deducono le seguenti
conclusioni:
, etc si deducono le seguenti
conclusioni:
- La densita' di probabilita' radiale mostra uno o piu' picchi (il
numero dei picchi e' pari a
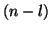 ) e
decade asintoticamente a zero (quindi, la probabilita' di trovare
l'elettrone a qualsiasi distanza dal nucleo non e' mai
esattamente nulla!)
) e
decade asintoticamente a zero (quindi, la probabilita' di trovare
l'elettrone a qualsiasi distanza dal nucleo non e' mai
esattamente nulla!)
- Per uno stesso valore di
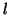 , il picco principale della densita'
di probabilita' radiale si sposta a distanza maggiore dal nucleo
all'aumentare di
, il picco principale della densita'
di probabilita' radiale si sposta a distanza maggiore dal nucleo
all'aumentare di 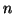 : in pratica, cio' significa che all'aumentare di
: in pratica, cio' significa che all'aumentare di
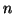 (cioe' dell'energia), l'elettrone si trova mediamente piu' lontano
dal nucleo.
(cioe' dell'energia), l'elettrone si trova mediamente piu' lontano
dal nucleo.
- Per uno stesso valore di
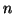 , il picco principale della densita'
di probabilita' radiale rimane approssimativamente alla stessa distanza
dal nucleo per diversi valori di
, il picco principale della densita'
di probabilita' radiale rimane approssimativamente alla stessa distanza
dal nucleo per diversi valori di 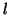 : quindi la distanza media
dell'elettrone dal nucleo non
dipende da
: quindi la distanza media
dell'elettrone dal nucleo non
dipende da 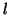
- Tuttavia, per uno stesso valore di
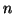 , in dipendenza da
, in dipendenza da 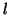 vi possono essere dei picchi secondari
di densita'
di probabilita' radiale: la distanza dal nucleo di tali picchi secondari
cresce con
vi possono essere dei picchi secondari
di densita'
di probabilita' radiale: la distanza dal nucleo di tali picchi secondari
cresce con 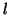 . Cio' viene interpretato come una diversa capacita' di
penetrazione degli elettroni verso il nucleo: in particolare, gli
elettroni
. Cio' viene interpretato come una diversa capacita' di
penetrazione degli elettroni verso il nucleo: in particolare, gli
elettroni 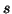 hanno una capacita' penetrativa maggiore di quella degli
elettroni
hanno una capacita' penetrativa maggiore di quella degli
elettroni 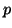 , che a loro volta possono avvicinarsi al nucleo piu'
efficacemente degli elettroni
, che a loro volta possono avvicinarsi al nucleo piu'
efficacemente degli elettroni 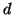 e cosi' via.
e cosi' via.



Next: Slide n. 103: l'andamento
Up: Slides delle lezioni del
Previous: Slide n. 101: la
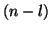 ) e
decade asintoticamente a zero (quindi, la probabilita' di trovare
l'elettrone a qualsiasi distanza dal nucleo non e' mai
esattamente nulla!)
) e
decade asintoticamente a zero (quindi, la probabilita' di trovare
l'elettrone a qualsiasi distanza dal nucleo non e' mai
esattamente nulla!)
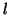 , il picco principale della densita'
di probabilita' radiale si sposta a distanza maggiore dal nucleo
all'aumentare di
, il picco principale della densita'
di probabilita' radiale si sposta a distanza maggiore dal nucleo
all'aumentare di 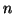 : in pratica, cio' significa che all'aumentare di
: in pratica, cio' significa che all'aumentare di
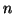 (cioe' dell'energia), l'elettrone si trova mediamente piu' lontano
dal nucleo.
(cioe' dell'energia), l'elettrone si trova mediamente piu' lontano
dal nucleo.
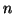 , il picco principale della densita'
di probabilita' radiale rimane approssimativamente alla stessa distanza
dal nucleo per diversi valori di
, il picco principale della densita'
di probabilita' radiale rimane approssimativamente alla stessa distanza
dal nucleo per diversi valori di 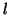 : quindi la distanza media
dell'elettrone dal nucleo non
dipende da
: quindi la distanza media
dell'elettrone dal nucleo non
dipende da 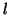
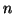 , in dipendenza da
, in dipendenza da 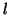 vi possono essere dei picchi secondari
di densita'
di probabilita' radiale: la distanza dal nucleo di tali picchi secondari
cresce con
vi possono essere dei picchi secondari
di densita'
di probabilita' radiale: la distanza dal nucleo di tali picchi secondari
cresce con 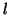 . Cio' viene interpretato come una diversa capacita' di
penetrazione degli elettroni verso il nucleo: in particolare, gli
elettroni
. Cio' viene interpretato come una diversa capacita' di
penetrazione degli elettroni verso il nucleo: in particolare, gli
elettroni 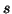 hanno una capacita' penetrativa maggiore di quella degli
elettroni
hanno una capacita' penetrativa maggiore di quella degli
elettroni 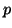 , che a loro volta possono avvicinarsi al nucleo piu'
efficacemente degli elettroni
, che a loro volta possono avvicinarsi al nucleo piu'
efficacemente degli elettroni 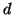 e cosi' via.
e cosi' via.