From 2000-06-27 it appears that in the system
![]() , the
, the
![]() reduction energy is more favorable than in
the corresponding
reduction energy is more favorable than in
the corresponding
![]() system. So let's do some
calcs without zirconia.
system. So let's do some
calcs without zirconia.
This refers to the
![]() system.
system.
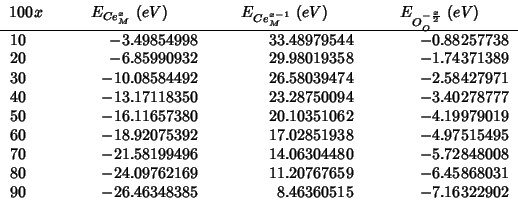
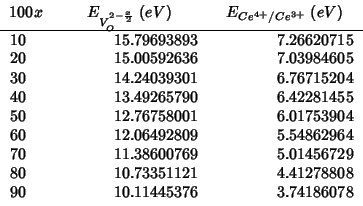
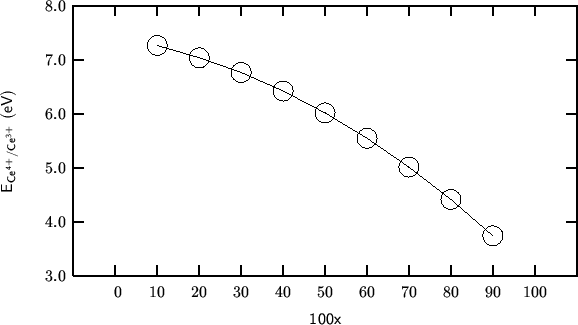
The
![]() reduction energy was evaluated according to
the procedure outlined in section 2000-06-21: even if the system does
not contain zirconia, the mean field analysis remains identical.
reduction energy was evaluated according to
the procedure outlined in section 2000-06-21: even if the system does
not contain zirconia, the mean field analysis remains identical.
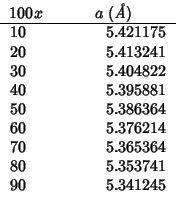
The following compares presently calculated lattice parameters with
the empirical equation of Kim (1989), which, for the present case
![]() , reads as:
, reads as:
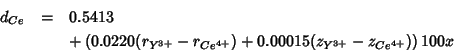
with ![]() and the
and the ![]() 's in
's in ![]() , or:
, or:
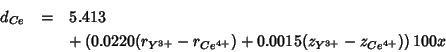
with ![]() and the
and the ![]() 's in Å.
's in Å.
The values of the various parameters are (Shannon, 1976):

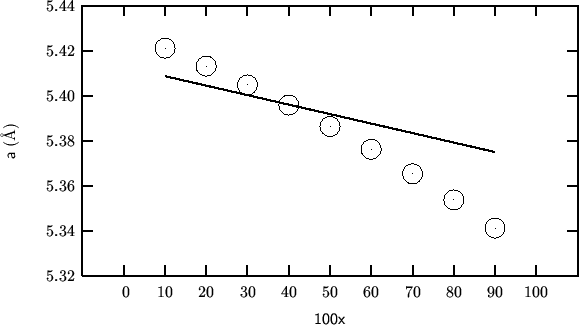
The accord does not seem to be very good, at least not as good as previously found.
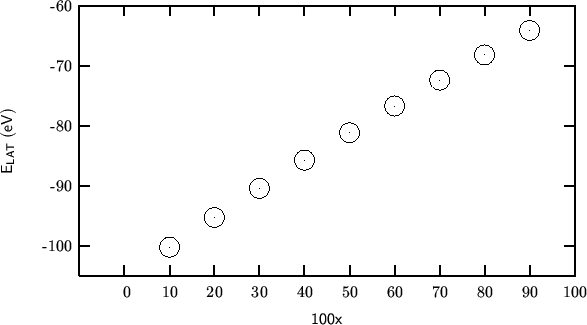
Note that ![]() decreases as the fraction of
decreases as the fraction of ![]() increases, notwithstanding that
increases, notwithstanding that
![]() . This
should be
due to the creation of oxygen vacancies. This is handled by the
. This
should be
due to the creation of oxygen vacancies. This is handled by the
![]() term in Kim's model: this is
negative for trivalent dopants so that it prevails if the
difference in radii is not large enough.
term in Kim's model: this is
negative for trivalent dopants so that it prevails if the
difference in radii is not large enough.

opti conp defect
maxcyc opt 200
maxcyc fit 200
dump every 1 ce4-30.dump
title
Ce4+ impurity
end
cell
5.329267 5.329267 5.329267 90.000000 90.000000 90.000000
fractional 5
Ce4 core 0.0000 0.0000 0.0000 -3.7000 0.7000 0.0000
Y core 0.0000 0.0000 0.0000 3.0000 0.3000 0.0000
O core 0.2500 0.2500 0.2500 0.0770 0.9250 0.0000
Ce4 shel 0.0000 0.0000 0.0000 7.7000 0.7000 0.0000
O shel 0.2500 0.2500 0.2500 -2.0770 0.9250 0.0000
space
225
size 9.0 20.0000
centre 0.00 0.00 0.00
impurity Ce4 0.00 0.00 0.00
species 2
Ce3 core -4.700000
Ce3 shel 7.700000
buck
Ce4 shel O shel 1986.8300 0.351070 20.400 0.000 15.000
Y core O shel 1345.1000 0.349100 0.0 0.000 15.000
Ce3 shel O shel 1731.6181 0.363720 14.433 0.000 15.000
O shel O shel 22764.300 0.149000 27.890 0.000 15.000
spring
Ce4 291.75000
Ce3 291.75000
O 27.290000