Determinazione del pKa per un acido moderatamente debole per via potenziometrica
esempio per lo ftalato acido di potassio II
C.Tavagnacco - versione 15.03.06
Dall’equazione di Henderson-Hasselbalch (H-H), pH = pKa + log ([A-]/[HA])
si ricava che quando [A-] = [HA] allora pH = pKa.
Questa osservazione permette di ricavare un metodo per la determinazione sperimentale per via potenziometrica del pKa di acido e basi moderatamente deboli.
Metodo
Per ricavare il pKa di un acido moderatamente debole si può agire nel modo seguente:
Si esegue la titolazione dell’acido debole con una base forte, si riportano i dati in tabella e si disegna la curva di titolazione come nell’esempio sotto riportato.
|
mL NaOH |
pH |
mL NaOH |
pH |
mL NaOH |
pH |
mL NaOH |
pH |
|
0 |
4.20 |
4.5 |
5.20 |
9.0 |
5.85 |
14 |
11.45 |
|
0.5 |
4.35 |
5 |
5.25 |
9.5 |
5.95 |
14.5 |
11.55 |
|
1 |
4.40 |
5.5 |
5.35 |
10 |
6.10 |
15 |
11.60 |
|
1.5 |
4.60 |
6 |
5.40 |
10.5 |
6.35 |
15.5 |
11.70 |
|
2 |
4.70 |
6.5 |
5.45 |
11 |
6.80 |
16 |
11.75 |
|
2.5 |
4.80 |
7 |
5.50 |
12 |
10.85 |
17 |
11.85 |
|
3 |
4.90 |
7.5 |
5.60 |
12.5 |
11.10 |
18 |
11.95 |
|
3.5 |
5.00 |
8 |
5.70 |
13 |
11.30 |
19 |
12.00 |
|
4 |
5.10 |
8.5 |
5.75 |
13.5 |
11.35 |
22 |
12.05 |
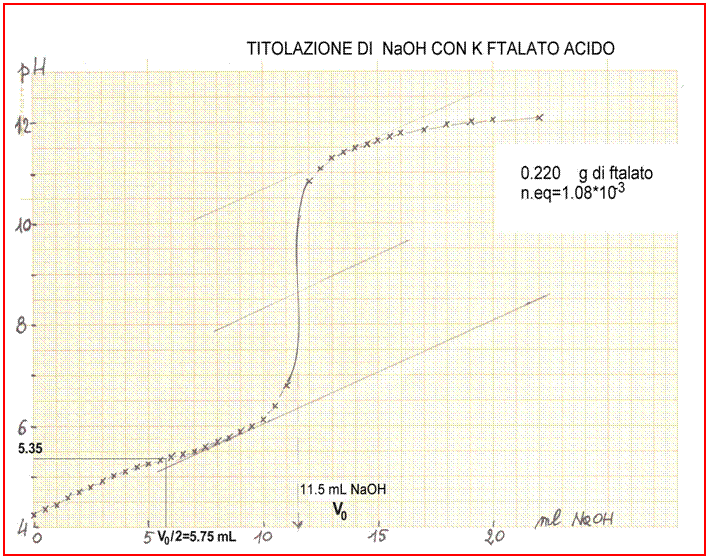
Nell’esempio riportato, 0.2200 g (pari a 1.08 × 10-3 equiv.) di ftalato acido di K sono messi in un becher e sono titolati con una soluzione di NaOH.
Si determinano il punto finale della titolazione, che corrisponde all' impiego di un certo volume V0 dibase forte, ed il punto di semi-titolazione V0/2. Dalla curva di titolazione si ricava V0 = 11.5 mL di NaOH.
Al punto equivalente:n.eqA = n.eqB1.08×10-3 equiv. = 11.5×10-3 L × NBNB = 0.094
È facile dimostrare che [A-] / [HA] = 1 (punto di semi-titolazione) quando il numero di equivalenti di titolante aggiunto è esattamente uguale a metà di quelli iniziali della sostanza da titolare, ovvero quando si è aggiunto esattamente un volume di titolante V0/2. Infatti:
HA + OH- --> A- + H2O
equiv. iniz. C0 0 0
equiv. aggiunti - x -
equiv. finali C0-x 0 x
N. equiv. di HA = n. equiv. A-, cioè [HA] = [A-] se C0 - x = x, cioè x = C0 / 2, cioè la quantità di OH- aggiunta = C0/2 a cui corrisponde il volume V0/2.
Per la determinazione del pKa è, dunque, necessario determinare prima graficamente V0 e poi interpolare sul grafico e leggere il valore del pH al quale V = V0/2.
Nel caso qui riportato V0 = 11.5 mL e quindiV0 / 2 = 11.5 / 2 = 5.75 mL. A tale volume il pH per interpolazione grafica = 5.35. Dunque l’acido in questione ha pKa = 5.35.
Tuttavia, questo metodo sfrutta solo il valore V0 / 2 e potrebbe essere poco accurato e preciso. È possibile aumentare l’accuratezza e la precisione del sistema se si considera che l’equazione di H-H è valida per punti attorno al valore in cui pH = pKa.
Inoltre l’equazione pH= pKa + log ([A-]/[HA])
equivale a quella di una retta y = q + mx
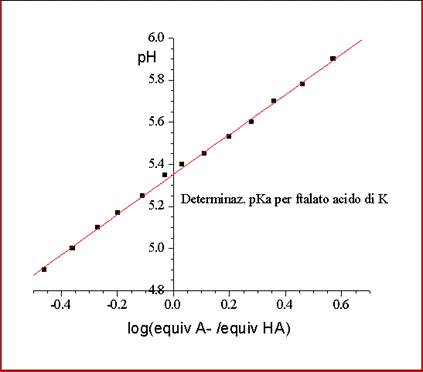
Se si riporta in grafico il pH in funzione di log ([A-]/[HA]) si ottiene una retta di pendenza 1 e di intercetta q= pKa.
Per quel che riguarda la quantità [A-]/[HA], dato che si tratta di un rapporto di concentrazioni di specie che si trovano nella stessa soluzione, il volume puo’ essere semplificato e nell’espressione si possono mettere il n. di equiv. di A- e di HA.
|
mL NaOH |
moli di A- × 10-3 |
moli di HA × 10-3 |
moli A- / moli HA |
log(A-/HA) |
pH |
|
3 |
.28 |
.80 |
.35 |
-.46 |
4.90 |
|
3.5 |
.33 |
.75 |
.44 |
-.36 |
5.00 |
|
4 |
.38 |
.70 |
.54 |
-.27 |
5.10 |
|
4.5 |
.42 |
.66 |
.64 |
-.20 |
5.20 |
|
5 |
.47 |
.61 |
.77 |
-.11 |
5.25 |
|
5.5 |
.52 |
.56 |
.93 |
-.03 |
5.35 |
|
|
.56 |
.52 |
1.08 |
.03 |
5.40 |
|
6.5 |
.61 |
.47 |
1.3 |
.11 |
5.45 |
|
7 |
.66 |
.42 |
1.57 |
.20 |
5.50 |
|
7.5 |
.71 |
.37 |
1.92 |
.28 |
5.60 |
|
|
.75 |
.33 |
2.27 |
.36 |
5.70 |
|
8.5 |
.80 |
.28 |
2.86 |
.46 |
5.75 |
|
9 |
.85 |
.23 |
3.70 |
.57 |
5.85 |
n. di equiv. di A- = n. equiv. di NaOH aggiunti = NNaOH× VNaOH: n. di equivdi HA = n. equiv iniziali di HA – quelli che hanno reagito (= n. equiv NaOH aggiunti).
Per poter disegnare la retta, si scelgono alcuni punti sperimentali (3 – 5 prima ed altrettanti dopo) dalla tabella 1, in un intervallo attorno al valore V0/2 (5.75 mL in questo specifico esempio), ad esempio tra 3 e 9 mL, e si costruisce una tabella come quella a fianco riportata come es.
Riportando in grafico il pH in funzione di log (n.equiv. A-/ n.equiv. HA) si ottiene una retta con pendenza = 0.95 (teorica = 1) ed intercetta = pKa = 5.35.
NOTA BENE: Risulta ovvio che l’equazione H-H è valida
nell’intorno del punto di semi-titolazione e non in quello di titolazione, inoltre quello qui riportato è solo
un esempio. Gli studenti devono tracciare il grafico e fare i
calcoli usando i loro dati ed applicando le formule, come
nell’esempio riportato, per 3 – 5 punti prima e 3 – 5
punti dopo il punto di semi-titolazione che loro trovano e non per quello
riportato in questo esempio !!!